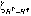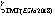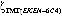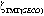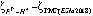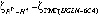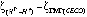В настоящее время мировым научным сообществом приняты рассчитанные три глобальные модели геоида: GECO [1, 2], EGM 2008 [1, 3] и EIGEN-6C4 [1, 4]. Исходя из указанного, используя географические информационные технологии (ГИС) и возможности обработки информации компьютеров, создана глобальная модель геоида в цифровом виде.
Теоретически изучаемая поверхность будет состоять из бесчисленного количества точек, поэтому исследователи часто создают геоид в виде сетки (Grid), путем распределения исследуемой территории уникальному значению ячейки сети модели геоида. Модель геоида имеет шаг сетки ΔB, ΔL и включает в себя набор значения высоты геоида. Расстояние между шагом указанной сетки представляет детализацию модели геоида. Точки на сетке имеют координаты (B, L, Н), а модель геоида сохраняется в общем цифровом формате *.GGF и используется в программах настройки GPS.
Из интернета или из файлов формы *.GGF мы можем легко использовать аномалию высоты любой точки, зная координаты B, L, но точность этих значений не соответствует требованиям определения высоты с помощью GPS измерений во Вьетнаме. Таким образом, нам, прежде всего, нужно оценить глобальную модель геопотенциала в исследуемой области, из которой выбрать соответствущую модель.
Методы оценки точности модели глобального геоида и результаты экспериментов, а также оценка глобальных геопотенциальных моделей и сравнение аномалий высот
Чтобы оценить точность в некоторой области, прежде всего, необходимо создать дубликаты данных GPS-нивелирования для точек равномерно распределенных по треритории этой области.
Геодезическая высота определяется технологией GPS в системе координат WGS-84 (HГ). Предположим, что в точках сети GPS одновременно с нормальной высотой (Hγ), определенной методом нивелирования, могут быть выявлены аномалии высоты [5]:
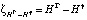. (1)
Различия между GPS-нивелированием и глобальной моделью геопотенциала ζГМГ по аномалии высоты получаем по формуле
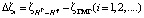, (2)
где i – общее количество точек.
Отклонение Δζi (2) содержит 3 типа ошибок: ошибка измерения GPS, ошибка нивелирования и ошибка глобальной геопотенциальной модели Δζi (набольшее значение, влияющее на итоговые вычисления).
Среднее отклонение мы получаем по формуле
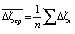. (3)
На основе отклонений Δζi также можно рассчитать среднее квадратическое отклонение аномалии высоты по формуле
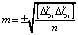. (4)
Точность результатов измерений оценивается средней квадратической ошибкой. Среднюю квадратическую ошибку вычисляем по формуле
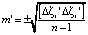, (5)
где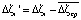 
.
Район исследования расположен на севере Вьетнама в географических границах: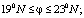 
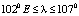(510 км×440 км).
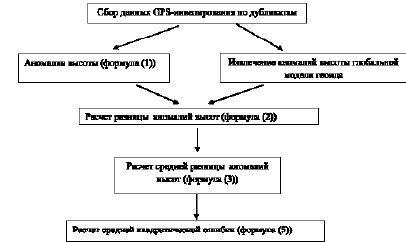
Рис. 1. Технологическая схема расчета оценки пригодности высоты геоида по глобальной модели и GPS-нивелирования на территории Вьетнама
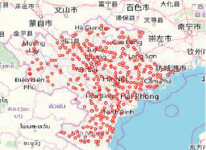
Рис. 2. Географическое распределение 302 пунктов GPS-нивелирования
Все наши оценочные тесты глобальной геопотенциальной модели (GGM), основанные на высотах геоида, относятся к 302 контрольным точкам (107 пунктов первого класса, 59 пунктов второго класса, 136 пунктов третьего класса), которые находятся на севере Вьетнама, в районе исследования (рис. 2).
Статистические значения данных об аномалиях высоты, которые использовались для оценки GGM, приведены в табл. 1.
Таблица 1
Аномалии высот: GPS-нивелирования и GGM (единицы измерения в метрах)
|
Аномалия высоты |
Минимальная |
Максимальная |
Средняя |
Средняя квадратическая ошибка |
|
|
-33,1677 |
-22,122 |
-27,175 |
2,289 |
|
|
-33,0050 |
-22,575 |
-27,603 |
2,266 |
|
|
-33,2367 |
-22,761 |
-27,672 |
2,255 |
|
|
-33,3481 |
-22,708 |
-27,672 |
2,272 |
Аномалии высоты GPS-нивелирования и GGM над исследуемой областью приведены на рис. 3.
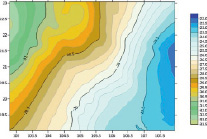
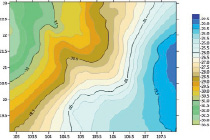
a) б)
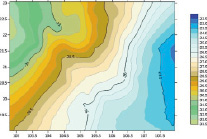
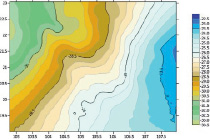
в) г)
Рис. 3. a) аномалии высоты на 302 пунктах GPS-нивелирования; б) аномалии высоты на 302 пунктах модели EGM 2008; в) аномалии высоты на 302 пунктах модели GECO; г) аномалии высоты на 302 пунктах модели EIGEN-6C4
Различия между GPS-нивелированием и глобальной моделью геопотенциала ζГМГ по аномалиям высот высчитываются по формуле (2).
Различия между GPS-нивелированием и глобальными моделями геопотенциала по аномалиям высот приведены в табл. 2.
Таблица 2
Отклонения значениий аномалии высот GPS-нивелирования и трех глобальных моделей геоида (GGM) на 302 пунктах
|
Аномалии высоты (м) |
Min отклонение (м) |
Мах отклонение (м) |
Сред. отклонение (м) |
Средняя квадратическая ошибка |
|
|
-0,5539 |
1,230 |
0,428 |
0,374 |
|
|
-0,2443 |
1,014 |
0,497 |
0,229 |
|
|
-0,1865 |
0,983 |
0,497 |
0,214 |
Заключение
Из табл. 2 очевидно, что модель GECO лучше всего подходит для данных, полученных из GPS-нивелирования, по сравнению с другими моделями в исследуемой области. Средняя квадратическая ошибка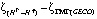 
меньше в 1,75 раза по сравнению с 
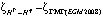, а также меньше в 1,07 раза по сравнению с 
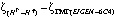. Различия аномалии высоты (
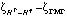) в исследуемой области показаны на рис. 4.
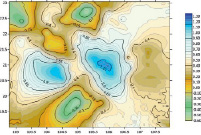
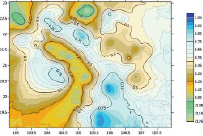
a) б)
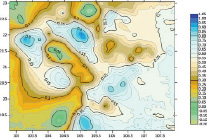
в)
Рис. 4. а) сравнительная оценка данных аномалии высот из GPS-нивелирования с аномалиями высот модели EGM 2008 на 302 пунктах; б) сравнительная оценка данных аномалии высот GPS-нивелирования с аномалиями высот модели EIGEN-6C4 на 302 пунктах; в) сравнительная оценка данных аномалии высот GPS-нивелирования с аномалиями высот модели GECO на 302 пунктах
Из результатов оценки GGM можно сделать вывод, что GECO может быть использована в качестве эталонной геоидной модели для дальнейшего определения локального квазигеоида на территории северного Вьетнама.