На стадии проектирования прецизионных сооружений атомных станций в перспективных пунктах их размещения создаются изыскательские геодинамические полигоны для изучения экзогенной и эндогенной геодинамики. Геодинамические полигоны создаются на местности в виде разветвленных высокоточных нивелирных сетей. Результаты повторного нивелирования таких сетей позволяют изучить в сжатые сроки (2–4 года) устойчивость оснований фундаментов проектируемых прецизионных объектов и кинематические характеристики современной геодинамики сооружений в сложившихся природных или природно-техногенных условиях.
При этом предъявляются особые требования как к совершенствованию постановки повторного нивелирования, так и к дальнейшему повышению уровня математической обработки рядов результатов нивелирования на основе разработки универсальных методов, обеспечивающих наилучшее приближение к неизвестной [1–3].
Целью исследования, представленного в статье, является разработка нового итерационного метода получения обобщенной средней (наилучшего приближения к неизвестной) из неравноточных результатов коррелированных измерений без обращения ковариационной матрицы, обладающего универсальностью при упрощении и снижении объемов вычислений по сравнению со стандартным походом [4–6].
Материалы и методы исследования
Суть метода состоит в том, что обобщённая средняя неравноточных измерений l1, l2, … , ln, как известно [4], определяется аналитическим выражением:
,
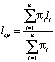где πi – обобщенный вес, равный сумме элементов i-й строки матрицы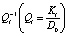 
;
Kl – ковариационная матрица результатов измерений; D0 – дисперсия единицы веса.
Рассмотрим один из вариантов представления погрешностей результатов измерений, представленных выражением: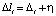 
, где Δi и η – случайные некоррелированные погрешности (Δi – индивидуальная погрешность, принадлежащая i-му результату li, а η – общая погрешность, входящая во все результаты наблюдений). Для такого случая разработан метод [4] установления обобщенной средней с оценкой ее точности.
В статье рассматривается итерационный метод получения обобщённой средней без обращения матрицы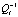 
, отличающийся универсальностью по отношению к методу, описанному в работах [4–6].
Результаты исследования и их обсуждение
Представим погрешность результатов наблюдений следующим аналитическим выражением:
,
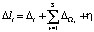где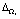 
– погрешность, входящая в множество наблюдений Ωr.
При этом условно, в качестве примера рассмотрим разветвленную нивелирную сеть (рисунок). В данной сети превышения между нивелирными пунктами i и A представлены величиной li; Δi – представляют ошибки превышений, полученных в секциях di; η – ошибка превышения в секции d16;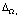 
– ошибки нивелирования в секции d10 и входящая в множество наблюдений Ω1 (l1, l2, l3).
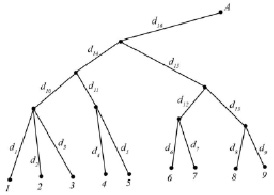
Схема разветвленной нивелирной сети
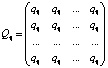
Рассмотрим матрицы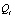 
, 
, 
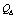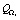и 
:
, 
,
, 
,
, 
, 
, 
.
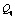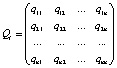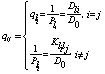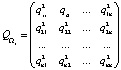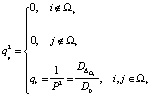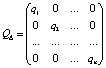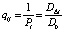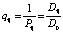При этом: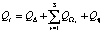 
.
Известно [4], что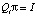 
, где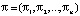 
; I – единичный вектор-столбец. Принимая это во внимание, получаем:
,
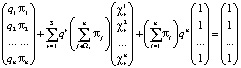где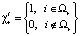 
– характеристическая функция множества Ωr.
Из аналитического выражения следует, что при каждом значении i = 1, 2, … , n справедливо равенство:
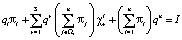. (1)
Обозначив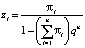 
в результате суммирования по 
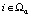, преобразуя равенство (1), получим:
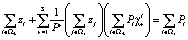. (2)
Из определения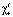 
следует, что:
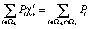, (3)
где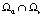 
представляет пересечение множеств Ωα и Ωr.
Применим обозначения: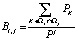 
, i = 1, 2, … , S; j = 1, 2, … , S; 
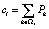, i = 1,2, … , S. В частности, 
.
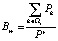Исходя из выражений (2) и (3), находим S неизвестных сумм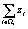 
:
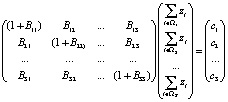. (4)
После обращения матрицы В: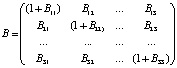 
и подстановки найденных решений 
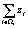(r = 1, 2, … , S) системы (4) в выражение (1), находим общие веса zi (i = 1, 2, … , n).
При этом отметим, что справедливо равенство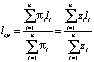 
и тот факт, что размерность В, равная S, значительно меньше размерности n-мерной матрицы Q.
Остановимся на предположении, что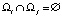 
, т.е. множества Ωi и Ωj дизъюнктные при i ≠ j. В этом случае В становится диагональной, и обратная матрица B–1 явным образом представляется как: 
.
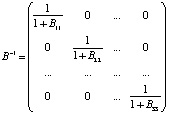Рассмотрим решения системы уравнений (4) в следующем виде:
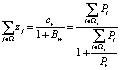. (5)
Представим формулу (1) с учетом выражения (5) в виде: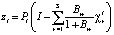 
.
Окончательно получим:
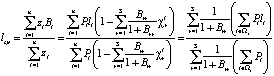. (6)
Рабочая формула (6) позволяет вычислить обобщённую среднюю в рассмотренном случае. В целях получения рекуррентной формулы для более общего случая, формулу (6) следует представить в другом виде. Для случая отсутствия ограничения общности предположим, что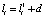 
, где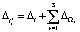 
; 
.
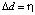В данном случае справедливо равенство:
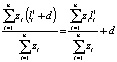. (7)
Приняв обозначение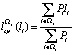 
, легко доказать:
.
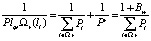И следовательно:
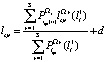. (8)
На основе формулы (8) можно построить для нахождения lcp рекуррентный процесс в более общей ситуации. Из вычисления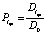 
получаем:
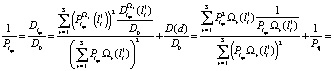
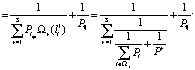
Предположим, что имеется двухиндексовое семейство множеств наблюдений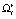 
, i = 1, 2, … , k; r = 1, 2, … , S и при фиксированном r при различных нижних индексах множества 
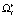не пересекаются, т.е. 
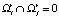, при i ≠ j, r = 1, 2, … , S. Обозначим Ωr(k) – единственное множество семейства 
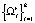, содержащее наблюдение lk.
Пусть:
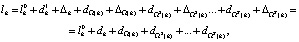
где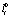 
, 
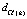вычисляются точно, а 
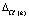(при r = 1, 2, … , S) – ошибки, принадлежащие множеству наблюдений Ωr(k).
Наконец, предположим, что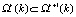 
для r = 1, 2, … , S-1 и k = 1, 2, … , n. Примем также, что ΩS(k) означает все множество наблюдений 
.
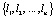Алгоритм вычислений
1. Вычисляем для усеченных наблюдений вида: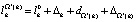 
. К обобщенных средних по множествам:
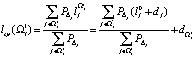; при i = 1, 2, … , k.
Далее вычисляем:
; 
; 
.
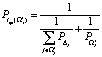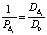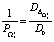2. Вычисляем на основании формулы (8):
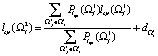, при i = 1, 2, … , k.
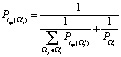, и так далее до последнего S-го шага.
Приведем пример расчета для нивелирной сети вида (рисунок).
На участках с превышением di число станций равно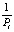 
. Выпишем систему множеств:
; 
; 
; 
;
; 
; 
.
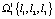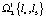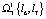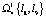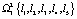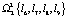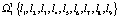Вычисляем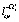 
, 
, 
, 
:
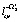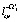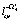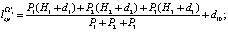
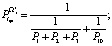
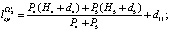
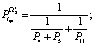
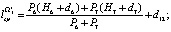
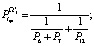
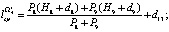
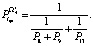
На втором этапе вычисляем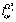 
, 
, 
, 
:
; 
;
; 
.
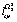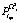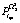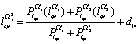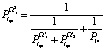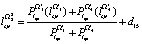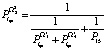Наконец, на последнем, третьем этапе вычисляем:
; 
.
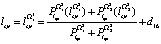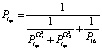В завершение заметим, что в соответствии с работой [4]:
,
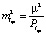где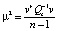 
, поэтому:
.
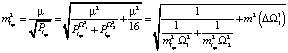В заключение следует отметить, что получены новые формулы для расчета обобщенной средней коррелированных измерений, не требующие обращения ковариационной матрицы измерений. При этом для разветвленных сетей нивелирования разработан итерационный метод расчета обобщенной средней, также не требующий обращения ковариационной матрицы.