Гидравлический разрыв пласта является одной из сложнейших операций в нефтегазодобывающей промышленности и наиболее эффективным методом повышения производительности скважин. Известно, что при проведении гидроразрыва пласта следует учитывать качество материала, закрепляющего трещину разрыва: диаметр, отсортированность и укладку зерен, градиенты фильтрации флюидов и другое. Однако проведение операции гидроразрыва пласта в некоторых случаях может сопровождаться неопределенностью в его эффективности, и перед началом работ требуется максимальное количество промысловых данных и дополнительных исследований [1; 2].
Цель исследования: с использованием лабораторной установки «Дарсиметр» по определению абсолютной проницаемости на искусственных образцах, представленных закрепляющим материалом трещин – песке и пропанте, с измеренным размером зерен определить коэффициенты проницаемости. Определить вид нелинейной или линейной связи градиента давления и расхода газа и применить по возможности двухчленную квадратичную зависимость Форхгеймера с расчетом полученных параметров. Cопоставить полученные измеренные значения проницаемости фракций с данным диаметром зерен с расчетными данными по определению проницаемости, исходя из зависимостей по литературным данным.
Материалы и методы исследования
Коэффициент проницаемости рассчитывается в случае линейной зависимости между давлением и расходом флюида по закону Дарси [3]. Однако закон Дарси – это эмпирический закон, и если на опыте допущение пропорциональности объёмного расхода градиенту давления не оправдывается, то считается, что градиент давления представляет собой некоторую функцию расхода, которую можно разложить в ряд Тейлора по степеням. Для реальных трещин при определении абсолютной проницаемости связь между градиентом давления и расходом при некоторых условиях может быть представлена зависимостью Форхгеймера:
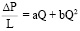 (1)
(1)
где а и b – вязкостной и инерционный коэффициенты сопротивления пористой среды, Q – объёмный расход газа через образец, ΔP/L – градиент давления
или 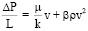 , (2)
, (2)
где μ – вязкость, k – проницаемость, β – инерционный коэффициент, v – скорость флюида.
В работах по нелинейной фильтрации ряд исследователей уточняют коэффициенты a и b в уравнении (1) или распространяют зависимость на различные случаи фильтрации [4; 5]. Коэффициенты не являются универсальными, и уравнение не отражает особенностей фильтрационных течений на различных режимах. Для уменьшения погрешностей при больших скоростях фильтрации Р.Д. Барри и М.В. Конвей используют в модели два дополнительных параметра – Kmr , принимающий значение от 0 до 1, и α, принимающий положительное значение. При крайних значениях параметра kmr предложенная зависимость приводится к законам Дарси или Форхгеймера [6]. В работе [7] описана методология определения проницаемости пористой среды, основанная на методе машинного обучения с использованием искусственных нейронных сетей и множественной регрессионной модели.
В настоящей работе для экспрессности получения результатов выбран метод расчета коэффициентов проницаемости [8] на основе зависимости Форхгеймера (1). Используя выражение, можно рассчитать
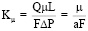 ,
,
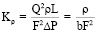 , (3)
, (3)
Kμ – вязкостной коэффициент, характеризует пропускную способность породы для вязкого флюида и площадь сечения поровых каналов, а Kρ – плотностной коэффициент, определяет пропускную способность породы для невязкого флюида и извилистость поровых каналов [8].
Для определения зависимости коэффициента проницаемости k от диаметра зерен cуществует ряд зависимостей, и коэффициент проницаемости зависит от распределения частиц по размеру, формы частиц и структуры упаковки. Проницаемость прямо пропорциональна квадрату размера частиц, умноженному на некоторую функцию пористости. Различными авторами приводятся виды функции пористости, которые могут изменять результат на 20 и более процентов. Для расчета проницаемости выбрана зависимость [9]:
k = d2 / 96σ, (4)
где σ = (5/4)*(1–m)2/m3.
Где пористость m может принимать значения от 0,259–0,476 в зависимости от упаковки зерен в данном образце и трещине. Без информации о значении коэффициента пористости и характере укладки частиц результаты расчетных значений при крайних значениях m=0,26-0,338 различаются в 3 раза. Число Рейнольдса Rе рассчитывалось по Щелкачеву В.Н.
Исследования проводились в искусственной кювете, куда помещался под уплотнением исследуемый материал. В качестве расклинивающих материалов для исследований использовался кварцевый песок Утевской и Чапаевской площадей и пропант марки «Боровичи» и «Форес». Для анализов материал песка был разделен на узкие фракции менее 63, 80, 106, 125, 150, 180 мкм. И 75 мкм, 125, 150, 196, 212, 212, 250, 350 мкм. Пропант на фракции 212, 390 мкм.
Результаты исследования и их обсуждение
Определение погрешностей коэффициента проницаемости проводилось на образцах керна Самотлорского месторождения и эталонах. Относительная погрешность для p=0,45-0,55 атм для 3-кратного измерения для эталона 5 мДарси составила k/kcр=2,3%, для p=1,5-1,7 атм составила 0,3%.
Исследование фильтрации газа через щели с раскрытостью от 47 до 200 мкм показало, что для щели 47 мкм зависимость градиента давления от расхода для диапазона 0,95-1,65 имеет линейный вид. C увеличением градиента давления снижается отношение k/b2, и среднее значение k/b2 для диапазона 0,95-1,65 составило 77510, а для диапазона p=0,37-1,72 это отношение cоставило 77820 против значения [10] =85000, и ниже значения [6] на 8%, что может быть объяснено различием в проведении опытов на различной аппаратуре и погрешностями. Для щели 96 мкм при линейной зависимости градиента давления от расхода среднее значение k/b2 составило 61015, что ниже отношения из [10] на 28%. Для щели 200 мкм значение k/b2 составило около 50% относительно полученного из [10], что может быть объяснено некорректностью расчетов из-за нелинейной зависимости градиента давления от расхода. Поэтому расчет проницаемости в зависимости от раскрытия щели, вероятно, возможен для щелей менее 100 мкм. Исследования фильтрации через капилляр показали нелинейную зависимость градиента давления от расхода газа. В координатах p/ql от q зависимость не выражается прямой линией, а представляет многочлен 3-й степени. Зависимость градиента давления от расхода газа выражается дробно-рациональной функцией q = x / (11,5+19,7p).
Таблица 1
Зависимости градиента давления Δp от расхода газа q и зависимость Δp/ql от q 1,04 атм. Коэффициент вариации для измеренных 7-кратных значений проницаемости на образцах Самотлорского месторождения составил 0,0014 при среднеквадратичном отклонении 0,062 и средней проницаемости 44,2 мД для давления
|
№ пп образца |
Название образца |
Зависимость градиента давления Δp от расхода q |
Зависимость Δp/ql от расхода q |
|
1 |
Чапаевская 63 |
-3*10-6x2+3*105x+7*10-7 |
2*1015x+2*1011 |
|
2 |
Чапаевская 80 |
-10-5x2+4*105x+8*10-7 |
1)1015x+9*1010 p=0,17-1 2) 3*1019x2-681013x+1011 p=0,17-1,3 |
|
3 |
Чапаевская 106 |
-10-5х2+6*10-5х+10-6 |
7*1014x+7*1010 |
|
4 |
Чапаевская 125 |
-3*10-5х2+9*10-5х-2*10-6 |
8*1014х+4*1010 |
|
5 |
Чапаевская 150 |
-3*10-5x2+9*105x+5*10-6 |
6*10`14x+3*1010 |
|
6 |
Чапаевская 180 |
-4*10-6x2+3*10-5x+8*10-6 |
2*1020x2-5*1015x+1011 |
|
7 |
Утевка |
-10 *10-5x2+5*10-5x+7*10-6 |
1) 2*1015x+4*1010 2) 2*1019x2-2*1014x+8*1010 |
|
8 |
Пропант Боровичи 1 |
-6*10-5x2+0,0001x+3*10-5 |
5*1014x-1010 |
|
9 |
Щель 1 – 47 мкм |
1)-7*10-6x2+4*10-5x-2*10-7 при диапазоне от 0,37-1,65 атм |
2*1019x2-7*1013+1011 |
|
2) 2*10-5x+10-5 при диапазоне от 0,95-1,65 атм |
- |
||
|
10 |
Щель 96 мкм |
0,0002x+10-5 |
- |
|
11 |
Щель 3 – 200 мкм |
9*10-8x2+5*10-8x+2*10-5 |
- |
|
12 |
Капилляр |
1) 10-6x2+4*10-6x+7*10-7 2) y=x/(11,5+19,7x) |
1) 3*10-17x+1011 для р=,24-0,96 2) 2*1029x3-2*1024x2+4*1018x+1012 для p=0,24-1,76 |
|
13 |
Пропант Форес |
-7*10-6x2+3*10-5x+10-6 |
4*1015x+1011 |
Рассмотрим зависимости градиента давления от расхода при фильтрации газа через изученные образцы. Для большинства образцов с расклинивающим материалом-песком и пропантом получены зависимости, которые нелинейны (табл. 1). Преобразование зависимостей в координатах p/ql от q представлены линейным уравнением для ряда случаев y=bx+a, где коэффициент a – вязкостной коэффициент сопротивления пористой среды – отрезок, отсекаемый прямой на оси p/ql, b – инерционный коэффициент пористой среды -тангенс угла наклона прямой к горизонтальной линии. Таким образом, были получены коэффициенты в уравнении Δp/L=aQ+bQ2. В таблице 2 приведены результаты расчета коэффициентов проницаемости Kµ и Kρ и коэффициентов а и b в уравнении для образцов песка площади Чапаевская, исходя из полученных зависимостей в координатах p/ql от q (табл. 1) и путем расчета коэффициентов проницаемости по зависимостям (3) при давлении в интервале p=1,08-1,33 атм.
Таблица 2
Вязкостной и плотностной коэффициенты проницаемости Kµ и Kρ , коэффициенты а и b в уравнении для образцов песка Чапаевской площади
|
D, мкм |
a*1010 |
b*1014 |
Kµ*10-12 |
Kρ*10-7 |
Δp |
Kµ*10-12 |
Kρ*10-7 |
Re |
|
По зависимостям табл. 1 |
Расчет при давлении Δp |
|||||||
|
63 |
20 |
20 |
2,3 |
4,06 |
1,33 |
3,3 |
1,2 |
22 |
|
80 |
9 |
10 |
5,14 |
8,11 |
1,08 |
4,7 |
2,0 |
30 |
|
106 |
7 |
7 |
6,61 |
11,6 |
1,28 |
6,1 |
4,0 |
53 |
|
125 |
4 |
8 |
11,6 |
10,1 |
1,21 |
7,3 |
5,5 |
67 |
|
150 |
3 |
6 |
15,4 |
13,5 |
1,21 |
8,6 |
7,6 |
85 |
Таблица 3
Вязкостной и плотностной коэффициенты проницаемости K µ и Kρ , коэффициенты а и b в уравнении для образцов песка Чапаевской и Утевской площади
|
Площадь |
Δp |
Kµ*10-12 |
Kρ*10-7 |
Re |
|
Чапаевская D=63 мкм |
0,18 |
4,2 |
0,3 |
4 |
|
0,286 |
3,7 |
0,3 |
6 |
|
|
0,47 |
3,8 |
0,6 |
10 |
|
|
0,837 |
3,5 |
0,9 |
15 |
|
|
1,33 |
3,3 |
1,2 |
22 |
|
|
1,495 |
3,1 |
1,2 |
23 |
|
|
1,61 |
3,2 |
1,4 |
26 |
|
|
Чапаевская D=125 мкм |
0,16 |
12,9 |
1,2 |
32 |
|
0,41 |
10,4 |
3,7 |
51 |
|
|
0,81 |
8,5 |
5,0 |
74 |
|
|
1,21 |
7,3 |
5,5 |
85 |
|
|
Чапаевская D=150 мкм |
0,197 |
15,1 |
3,8 |
32 |
|
0,405 |
12,8 |
5,6 |
51 |
|
|
0,8 |
10,4 |
7,3 |
74 |
|
|
1,211 |
8,6 |
7,6 |
85 |
|
|
Утевская (общая) |
1,46 |
5,1 |
3,2 |
47 |
|
1,007 |
6,0 |
3,1 |
41 |
|
|
0,964 |
6,1 |
3,0 |
40 |
|
|
0,516 |
7,6 |
2,5 |
30 |
С увеличением диаметра зерен коэффициенты проницаемости Kµ и Kρ возрастают при увеличении значения числа Рейнольдса. Различия в полученных значениях этими способами обусловлены тем, что расчет в первом случае брался по диапазону 0,2-1,5 атм, а во втором случае на режиме p=1,08-1.,33 атм. Далее были рассчитаны коэффициенты проницаемости Kµ и Kρ при давления Δp и размере диаметра зерен D (табл. 3, 4). C увеличением диаметра зерен при возрастании градиента давления Kµ снижается, а изменение коэффициента Kρ не имеет выраженной тенденции при увеличении числа Re.
Сравнение значений коэффициента проницаемости, рассчитанного по формуле (3), и измеренных значений (табл. 5-7) показало, что для фракций Чапаевского месторождения измеренные значения попадают в интервал рассчитанных значений проницаемости K для интервала возможных значений пористости m=0,26-0,336. Для образцов Утевской площади характерен больший диаметр зерен во фракциях от 75 до 196 мкм, чем для Чапаевской площади, в которой интервал фракций варьирует от 63 до 150 мкм. Cравнение значений коэффициента проницаемости рассчитанного по формуле (3) и измеренных значений для Утевской площади показало их совпадение для интервала до 150 мкм, а при значениях диаметра более 150 мкм измеренные значения меньше рассчитанных значений интервала тем больше, чем больше диаметр зерен фракции и меньше рассчитанных от 2 до 8 раз. Поэтому расчет по формуле (3) для исследуемых образцов справедлив при диаметре фракции до 150 мкм.
Таблица 4
Вязкостной и плотностной коэффициенты проницаемости Kµ и Kρ для образцов пропанта «Боровичи»
|
№ |
d |
Δp |
Kµ*10-12 |
K ρ*10-7 |
Re |
|
1 |
390 мкм |
0,16 |
30,2 |
26,9 |
109 |
|
0,33 |
19,4 |
23,8 |
118 |
||
|
0,49 |
15,5 |
22,2 |
124 |
||
|
0,68 |
12,8 |
21,2 |
130 |
Таблица 5
Измеренные и рассчитанные значения проницаемости для образцов пропанта «Боровичи» при диаметре частиц 390 и 212 мкм
|
D, мкм |
ΔP, атм |
K изм*10-12 |
K*10-12, диапазон от m=0,26–0,336 |
|
212 |
0,5 |
4 |
4,17-11,6 |
|
390 |
0,5 |
15 |
40-361 |
Таблица 6
Измеренные и рассчитанные значения проницаемости для образцов песка месторождения Чапаевское
|
D, мкм |
ΔP, атм |
K изм*10-12 |
K*10-12, диапазон от m=0,26–0,336 |
|
63 |
0,47 |
2,9 |
1-2,9 |
|
80 |
0,456 |
4,4 |
1,7-4,76 |
|
106 |
0,411 |
6,2 |
3-8,36 |
|
125 |
0,411 |
7,9 |
4,17-11,6 |
|
150 |
0,405 |
9,8 |
6-16,7 |
Таблица 7
Измеренные и рассчитанные значения проницаемости для образцов песка месторождения Утевское
|
D, мкм |
ΔP, атм |
K изм*10-12 |
K *10-12, диапазон от m=0,26–0,336 |
|
75 |
0,54 |
2,2 |
1,5-4,18 |
|
125 |
0,54 |
4,3 |
4,17-11,6 |
|
150 |
0,511 |
3,9 |
6-16,7 |
|
196 |
0,543 |
5,5 |
от 10 до 28 |
|
212 |
0,54 |
4,7 |
12-33 |
|
250 |
0,54 |
3,3 |
16,7-46 |
|
350 |
0,55 |
4,3 |
32-91 |
Расчет коэффициентов проницаемости Kµ и Kρ зависит от выбора режима измерений и погрешностей при аппроксимации кривых в координатах p/ql от q. Поэтому данным способом можно оценить коэффициенты проницаемости экспрессно и приближенно, с определенной долей погрешности. Таким образом, следует учитывать при проектировании процесса гидроразрыва пласта cвойства закрепляющего материала: диаметр зерен, их укладку, от которых зависит проницаемость образующихся трещин. Данные исследования на моделях закрепляющего материала трещин могут являться дополнением к обоснованию рисков проведения гидроразрыва пласта.



