На сегодняшний день существуют различные методы спутникового позиционирования, в том числе инновационные. Одним из таких методов является Precise Point Positioning или, по-другому, метод высокоточных координат определений (далее «РРР») [1].
Метод точного позиционирования (далее «РРР») относится к абсолютным определениям местоположения, основан на применении спутниковой корректирующей информации, содержащей поправки к эфемеридам и времени бортовых часов навигационных спутников и атмосферных поправок в пределах локальной области, позволяющий определять пространственные координаты объектов с достаточно высокой точностью.
Помимо этого существует следующая классификация РРР-методов:
PPP (Float PPP) – реализация метода без разрешения целочисленной неоднозначности псевдофазовых измерений.
РРР-AR (Interger PPP) – с разрешением целочисленной неоднозначности псевдофазовых измерений.
РРР-RTK – с разрешением целочисленной неоднозначности псевдофазовых измерений и использованием атмосферных коррекций в пределах локальной области.
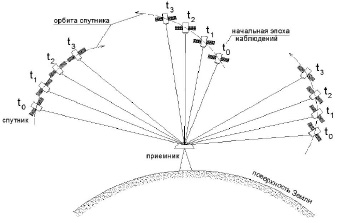
Рис. 1. Схема РРР-метода
Метод РРР можно реализовать как в апостериорном режиме, так и в режиме реального времени. В первом случае результат получают в процессе камеральной обработки или с помощью специализированных сервисов.
Для точного определения пространственного положения точки метод РРР используется ионосферно-свободная комбинация двух несущих частот [2, 3]. В общем виде для одного спутника и приемника комбинации представлены в виде формулы
PiA = ρ + c(dt – dT) + Tr + εp
Фif = ρ + c(dt – dT) + Tr + NΛ + εФ
где Фif PiA – ионосферная комбинация несущих фаз (L1, L2) и псевдодальностей (Р1,Р2); dt, dT – ошибка часов приемника и спутника (так называемый сдвиг шкал относительно системной шкалы времени (далее «СШВ»)); c – скорость распространения радиоволн в вакууме; Tr – тропосферная задержка; N – целочисленные колебания несущей фазы; Λ – длина несущей волны; εp, εФ – различные шумовые компоненты, включающие многолучевость (многопутность), ρ – расстояние между спутником и приемником.
На рис. 1 изображена обобщенная схема РРР-методов.
Для получения устойчивого решения при использовании РРР-метода необходимо, чтобы продолжительность измерений составляла не менее 2 ч. Однако существует возможность обработки и 10-минутных измерений, но в таком случае получается неточное решение. Помимо этого, частота записи должна составлять не менее 10 с [2].
На сегодняшний день существуют два подхода к обработке по РРР-алгоритму: с использованием программных обеспечений и интернет-сервисов. В качестве программных обеспечений можно выделить следующие: Trimble Business Centre (далее «TBC»), КРЕДО ГНСС, RTK LIB. Среди интернет-сервисов – Trimble RTX, APPS, CRSR, magic GNNS. В каждом из интернет-сервисов предоставляется бесплатный, не ограниченный по времени доступ в отличие от программных обеспечений [3].
Цели исследования:
1. Сравнить результаты обработки в статике и РРР при многократных спутниковых измерениях.
2. Проанализировать влияние продолжительности измерений на получаемые разности приращений координат.
3. Проанализировать влияние pdop фактора и количества принимаемых спутников на получаемые разности приращений координат.
Материалы и методы исследования
В качестве экспериментальной модели была сформирована спутниковая сеть, состоящая из 5 пунктов. 4 пункта сети входят в состав сети базовых станций EFT-COORS, где были получены RINEX [4–7]. В свою очередь, эталонные координаты 5 пункта получены самостоятельно при использовании двухчастотного спутникового приемника Trimble R10.
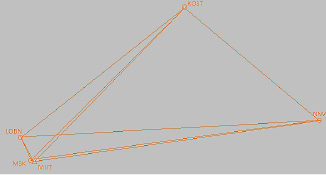
Рис. 2. Схема спутниковой сети
На рис. 2 изображена спутниковая сеть, включающая в себя 5 пунктов.
Пункты спутниковой сети находятся на расстояниях от 4 (MSK-MIIT) до 409 (LOBN-NNV) км. Средние расстояния между пунктами – 210 км.
В свою очередь измерения производились по 3 часа каждый день в течение 12 дней. Для обработки данных по РРР-алгоритму было использовано два интернет-сервиса Trimble RTX и CRSR [8]. Основываясь на координатах, были получены приращения координат. В дальнейшем были определены разности приращений координат между определенными и эталонными приращениями.
Помимо этого, были определены координаты с использованием CRSR, после чего были высчитаны приращения и разности приращений координат [9].
Для контроля получаемых разностей приращений координат была выполнена обработка базовых линий (векторов) с добавлением высокоточных (финальных) эфемерид в программном обеспечении КРЕДО ГНСС [10]. В качестве исходного (опорного) пункта был выбран пункт МИИТ.
Результаты исследования и их обсуждение
В табл. 1 и 2 приводится сравнение усредненных разностей приращений координат; в табл. 3 и 4 – максимальные разности приращений координат; в табл. 5 и 6 – минимальные разности.
Таблица 1
Сравнение средних разностей приращений координат при продолжительности измерений 1 час
|
Линия |
Статика – КРЕДО |
РРР-RTX |
РРР-CRSR |
||||||
|
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
|
|
MSK-MIIT |
0,019 |
-0,002 |
-0,035 |
0,012 |
-0,009 |
0,014 |
0,014 |
-0,010 |
0,015 |
|
KOST-MIIT |
-0,021 |
0,025 |
0,009 |
0,000 |
-0,002 |
-0,011 |
0,006 |
0,004 |
0,000 |
|
LOBN-MIIT |
0,041 |
0,036 |
-0,034 |
0,004 |
-0,005 |
-0,002 |
0,004 |
0,000 |
0,030 |
|
NNV-MIIT |
0,008 |
0,014 |
0,008 |
-0,001 |
0,007 |
-0,003 |
0,014 |
0,021 |
0,033 |
|
MSK-KOST |
0,031 |
-0,029 |
-0,020 |
0,012 |
-0,006 |
0,025 |
0,008 |
-0,014 |
0,015 |
|
MSK-LOBN |
0,000 |
-0,033 |
-0,014 |
0,008 |
-0,004 |
0,016 |
0,010 |
-0,010 |
-0,014 |
|
MSK-NNV |
0,012 |
-0,013 |
-0,012 |
0,014 |
-0,016 |
0,017 |
0,001 |
-0,031 |
-0,017 |
|
KOST-LOBN |
-0,034 |
0,002 |
-0,007 |
-0,004 |
0,003 |
-0,009 |
0,002 |
0,004 |
-0,030 |
|
KOST-NNV |
0,021 |
-0,014 |
-0,008 |
0,002 |
-0,010 |
-0,008 |
-0,008 |
-0,018 |
-0,033 |
|
LOBN-NNV |
0,007 |
0,020 |
0,007 |
0,006 |
-0,012 |
0,001 |
-0,010 |
-0,021 |
-0,003 |
Таблица 2
Сравнение средних разностей приращений координат при продолжительности измерений 2 часа
|
Линия |
Статика – КРЕДО |
РРР-RTX |
РРР-CRSR |
||||||
|
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
|
|
MSK-MIIT |
0,020 |
0,001 |
-0,031 |
0,012 |
-0,007 |
0,004 |
0,010 |
-0,008 |
0,001 |
|
KOST-MIIT |
-0,008 |
-0,018 |
0,003 |
0,002 |
0,002 |
-0,014 |
0,010 |
0,013 |
0,008 |
|
LOBN-MIIT |
-0,001 |
0,023 |
0,037 |
0,005 |
-0,001 |
-0,007 |
0,005 |
0,008 |
0,008 |
|
NNV-MIIT |
-0,008 |
0,003 |
0,012 |
-0,002 |
0,010 |
-0,008 |
0,003 |
0,015 |
-0,007 |
|
MSK-KOST |
0,014 |
-0,021 |
-0,001 |
0,010 |
-0,009 |
0,018 |
0,000 |
-0,022 |
-0,007 |
|
MSK-LOBN |
-0,007 |
0,003 |
-0,012 |
0,006 |
-0,006 |
0,010 |
0,005 |
-0,017 |
-0,007 |
|
MSK-NNV |
0,041 |
0,046 |
0,048 |
0,014 |
-0,017 |
0,012 |
0,007 |
-0,024 |
0,008 |
|
KOST-LOBN |
-0,033 |
0,015 |
0,014 |
-0,004 |
0,003 |
-0,008 |
0,005 |
0,005 |
0,000 |
|
KOST-NNV |
-0,015 |
-0,012 |
-0,033 |
0,004 |
-0,008 |
-0,006 |
0,006 |
-0,002 |
0,015 |
|
LOBN-NNV |
0,028 |
0,052 |
0,065 |
0,008 |
-0,011 |
0,002 |
0,002 |
-0,007 |
0,015 |
Таблица 3
Сравнение максимальных разностей приращений координат при продолжительности измерений 1 час
|
Линия |
Статика – КРЕДО |
РРР-RTX |
РРР-CRSR |
||||||
|
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
|
|
MSK-MIIT |
0,020 |
0,001 |
-0,032 |
0,024 |
-0,001 |
0,037 |
0,028 |
0,001 |
0,033 |
|
KOST-MIIT |
-0,018 |
0,064 |
0,036 |
0,010 |
0,003 |
0,000 |
0,015 |
0,011 |
0,007 |
|
LOBN-MIIT |
0,043 |
0,043 |
0,059 |
0,013 |
0,003 |
0,017 |
0,016 |
0,023 |
0,048 |
|
NNV-MIIT |
0,016 |
0,044 |
0,018 |
0,005 |
0,015 |
0,020 |
0,028 |
0,039 |
0,047 |
|
MSK-KOST |
0,049 |
0,005 |
-0,002 |
0,017 |
-0,001 |
0,037 |
0,013 |
-0,009 |
0,027 |
|
MSK-LOBN |
0,010 |
-0,003 |
0,010 |
0,015 |
0,002 |
0,030 |
0,021 |
0,005 |
0,010 |
|
MSK-NNV |
0,058 |
0,047 |
0,041 |
0,021 |
-0,010 |
0,044 |
0,006 |
-0,024 |
0,010 |
|
KOST-LOBN |
-0,029 |
0,003 |
0,016 |
0,008 |
0,011 |
0,005 |
0,014 |
0,016 |
-0,003 |
|
KOST-NNV |
0,028 |
-0,012 |
-0,006 |
0,009 |
-0,006 |
0,014 |
0,005 |
-0,010 |
-0,012 |
|
LOBN-NNV |
0,017 |
0,057 |
0,049 |
0,010 |
-0,007 |
0,023 |
-0,003 |
-0,002 |
0,009 |
Таблица 4
Сравнение максимальных разностей приращений координат при продолжительности измерений 2 часа
|
Линия |
Статика – КРЕДО |
РРР-RTX |
РРР-CRSR |
||||||
|
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
|
|
MSK-MIIT |
0,025 |
0,001 |
-0,027 |
0,022 |
-0,002 |
0,014 |
0,014 |
-0,006 |
0,014 |
|
KOST-MIIT |
-0,004 |
0,003 |
0,006 |
0,008 |
0,007 |
-0,007 |
0,021 |
0,022 |
0,029 |
|
LOBN-MIIT |
0,002 |
0,030 |
0,040 |
0,010 |
0,007 |
0,003 |
0,018 |
0,040 |
0,028 |
|
NNV-MIIT |
-0,001 |
0,010 |
0,020 |
0,004 |
0,015 |
0,000 |
0,010 |
0,031 |
0,028 |
|
MSK-KOST |
0,022 |
0,023 |
0,020 |
0,018 |
-0,003 |
0,025 |
0,011 |
-0,012 |
0,014 |
|
MSK-LOBN |
-0,005 |
0,004 |
-0,010 |
0,013 |
0,003 |
0,014 |
0,025 |
0,002 |
0,012 |
|
MSK-NNV |
0,041 |
0,046 |
0,050 |
0,018 |
-0,014 |
0,018 |
0,016 |
-0,010 |
0,048 |
|
KOST-LOBN |
-0,032 |
0,018 |
0,017 |
0,000 |
0,007 |
-0,002 |
0,023 |
0,024 |
0,016 |
|
KOST-NNV |
-0,013 |
0,029 |
0,012 |
0,007 |
-0,005 |
0,002 |
0,014 |
0,010 |
0,037 |
|
LOBN-NNV |
0,038 |
0,052 |
0,072 |
0,011 |
0,000 |
0,008 |
0,012 |
0,032 |
0,036 |
Таблица 5
Сравнение минимальных разностей приращений координат при продолжительности измерений 1 час
|
Линия |
Статика – КРЕДО |
РРР-RTX |
РРР-CRSR |
||||||
|
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
|
|
MSK-MIIT |
0,016 |
-0,004 |
-0,035 |
0,004 |
-0,022 |
-0,015 |
0,004 |
-0,022 |
-0,002 |
|
KOST-MIIT |
-0,042 |
0,015 |
0,004 |
-0,008 |
-0,015 |
-0,040 |
0,000 |
-0,005 |
-0,010 |
|
LOBN-MIIT |
0,033 |
0,035 |
-0,042 |
-0,009 |
-0,019 |
-0,033 |
-0,013 |
-0,021 |
0,008 |
|
NNV-MIIT |
-0,058 |
0,009 |
0,007 |
-0,011 |
-0,004 |
-0,037 |
-0,002 |
0,008 |
0,017 |
|
MSK-KOST |
0,027 |
-0,032 |
-0,022 |
0,002 |
-0,009 |
0,015 |
0,001 |
-0,019 |
0,003 |
|
MSK-LOBN |
-0,005 |
-0,036 |
-0,016 |
0,000 |
-0,012 |
0,005 |
-0,001 |
-0,029 |
-0,043 |
|
MSK-NNV |
0,006 |
-0,019 |
-0,017 |
0,006 |
-0,024 |
0,004 |
-0,013 |
-0,039 |
-0,041 |
|
KOST-LOBN |
-0,037 |
-0,010 |
-0,009 |
-0,011 |
-0,004 |
-0,021 |
-0,008 |
-0,020 |
-0,057 |
|
KOST-NNV |
-0,008 |
-0,036 |
-0,031 |
-0,005 |
-0,016 |
-0,021 |
-0,017 |
-0,028 |
-0,054 |
|
LOBN-NNV |
-0,076 |
0,016 |
0,003 |
-0,003 |
-0,022 |
-0,012 |
-0,031 |
-0,034 |
-0,016 |
Таблица 6
Сравнение минимальных разностей приращений координат при продолжительности измерений 2 часа
|
Линия |
Статика – КРЕДО |
РРР-RTX |
РРР-CRSR |
||||||
|
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
δX, м |
δY, м |
δZ, м |
|
|
MSK-MIIT |
0,018 |
-0,001 |
-0,032 |
0,005 |
-0,012 |
-0,005 |
0,005 |
-0,011 |
-0,016 |
|
KOST-MIIT |
-0,033 |
-0,022 |
-0,012 |
-0,003 |
-0,001 |
-0,023 |
-0,004 |
0,005 |
-0,011 |
|
LOBN-MIIT |
-0,003 |
-0,022 |
0,007 |
0,002 |
-0,006 |
-0,016 |
-0,013 |
-0,011 |
-0,018 |
|
NNV-MIIT |
-0,057 |
-0,022 |
-0,051 |
-0,009 |
0,004 |
-0,015 |
-0,005 |
0,004 |
-0,038 |
|
MSK-KOST |
0,008 |
-0,027 |
-0,003 |
0,004 |
-0,012 |
0,012 |
-0,009 |
-0,030 |
-0,025 |
|
MSK-LOBN |
-0,012 |
0,001 |
-0,013 |
0,001 |
-0,016 |
0,006 |
-0,009 |
-0,048 |
-0,025 |
|
MSK-NNV |
0,034 |
0,042 |
0,036 |
0,010 |
-0,021 |
0,005 |
-0,001 |
-0,040 |
-0,015 |
|
KOST-LOBN |
-0,033 |
0,015 |
0,013 |
-0,007 |
-0,005 |
-0,013 |
-0,005 |
-0,030 |
-0,012 |
|
KOST-NNV |
-0,015 |
-0,016 |
-0,039 |
-0,003 |
-0,012 |
-0,013 |
0,001 |
-0,018 |
-0,010 |
|
LOBN-NNV |
-0,074 |
0,049 |
0,043 |
0,004 |
-0,017 |
-0,006 |
-0,009 |
-0,024 |
-0,017 |
При трех часах были получены практически такие же результаты, что и при двух часах. Наибольшие разности составили 5 мм; наименьшие – 3 мм.
При двух часах были выявлены максимальные разности. В сравнении двух- и трехчасовых данных отличаются в среднем на 2–3 мм
Отклонение минимальных разностей по модулю составило в среднем 2–3 мм для минимальных разностей приращений координат в сравнении с треххчасовыми измерениями.
Анализируя табл. 1–6, можно заметить, что приращения координат в среднем отличаются на 2–3 мм при сравнении двух- и трехчасовых измерений соответственно. При этом стоит отметить, что pdop в среднем составил 1.54+-0,03 Количество принимаемых спутников при одном часе в среднем составило 18; при двух часах – 24, при трех часах – 27.
На основании табл. 1–6 был построен график (рис. 3), иллюстрирующий влияние продолжительности измерений на получаемые результаты.
В работе [10] отмечено, что при продолжительности измерений 1 час расхождения достигают 3 см при расстоянии в 50 км; при продолжительности 2 часа не более 7 мм по δZ; 3 и 4 ч – расхождения между приращениями координат не превышали 2 мм. В работе [11] было рассмотрено применение РРР-методов для решения задач геодинамики, где было отмечено, что относительный метод проигрывает в плане точности РРР-методам.
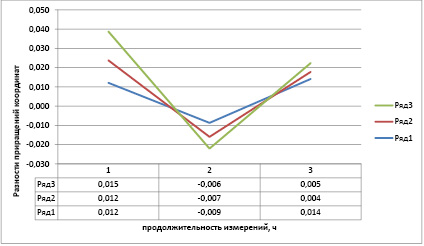
Рис. 3. Распределение разностей приращения
Выводы
1. Точность взаимного положения пунктов, определенных РРР-методами, не зависит от расстояний между пунктами.
2. По РРР-алгоритму возможно обрабатывать и 10-минутные измерения. Однако для получения уточненного решения продолжительность измерений должна составлять не менее 2 ч. При продолжительности измерений 3 ч и более точность взаимного положения пунктов практически не меняется.
3. При многократных измерениях получается примерно одинаковая точность как взаимного положения пунктов, так и одиночного положения пунктов при наличии эталонных координат



