Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

Картографическая проекция Ламберта в Сирии использует равноугольную проекцию, которая сохраняет углы при переходе от эллипса к поверхности проекции. Эта проекция была разработана французом (Дураффурад), который использовал базовые точки (тригонометрическую сетку) первого и второго ранга в расчетах, он использовал географические координаты, из которых он вывел прямоугольные координаты, используя формулу преобразования [1].

В рамках этой системы все карты были созданы до 1958 г. Военно-геодезическим управлением (в настоящее время Главное управление геодезических работ) в масштабе 1:25000 и 1:50 000, из которых были получены карты меньшего масштаба. Контрольные точки системы (которая простиралась от северного Алеппо до равнин Хорана на юге и от побережья на западе до окраин пустыни на востоке) послужили отправной точкой для их уплотнения российскими геодезистами, создавшими карты всех сирийских земель в конце 1950-х гг. на масштаб 1:200 000 по контракту с Министерством промышленности и торговли. Был использован эллипсоид Кларка 1880 г. [2].

В работе ставится цель совершенствования координатной основы Республики Сирии. На основе спутниковых наблюдений показать, как можно определить состояние сирийской системы координат Ламберта; параметры трансформации и уравнение регрессии для преобразования геодезических координат, измеренных с помощью GPS, в геодезические координаты на эллипсе Кларка 1880.

Материалы и методы исследования

Анализ и обобщение теоретических и практических результатов исследований при обосновании актуальности темы работы и решаемых задач, включающие экспериментальные геодезические спутниковые измерения, методы математической статистики и теории вероятностей, в том числе метод наименьших квадратов при обработке спутниковых определений.

Анализ современного состояния системы координат Ламберта в Сирии

Проекционная поверхность. Прямая коническая касательная к широте 38,5°, а поскольку сирийская территория расположена в пределах шести широт, трех северных и южных широт, то есть в пределах 35,5° и 41,5°, и был использован K0 = 0,99962560 для снижения линейных искажений, и деформации нет на двух широтах рядом с городами (Алеппо и Аль-Санамайн) [1, 3]:

40.25 = 1.75 + 38.5 = 1φгр.

36,75 = 1,75 – 38 = 2φгр.

Точка перспективы расположена в центре Земли, и, поскольку эта проекция является равноугольной, она зависит от математических формул в процессе проектирования. Географические координаты центра проекции:

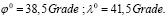
Прямоугольная система. В сирийской конической проекции Ламберта ось y применяется к долготе, спроецированной графикой, проходящей через центр системы, а направление x с запада на восток перпендикулярно ей, что относительно широты, проходящей через центр системы, И для различения прямоугольной системы в сирийской конической проекции Ламберта из прямоугольной стереографической проекционной системы, так что все территории находятся в первой четверти и все координаты точек становятся положительными, центр системы координат (x, y) был перемещен на 300 км к западу и югу [3].

X = x + 300KM; Y = y + 300Km;

x = R sinγ; y = R0-Rcosγ.

Координаты с помощью этой системы с учетом коэффициента искажения следующим образом [4, 5]:

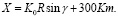
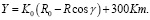
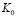= 0.99962560.

.

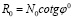Экваториальный радиус кривизны первого вертикала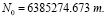

,

,

.

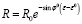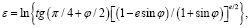
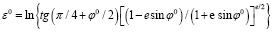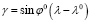И тоже можно вычислить с помощью двух формул

,

.

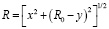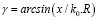Масштабный коэффициент для точки или расстояния в несколько километров составляет

,

,

,

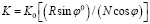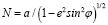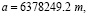
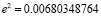где a – большая полуось; b – малая полуось; е2 – первый эксцентриситет; N – экваториальный радиус; f – геометрическое (полярное) сжатие; k0 – масштабный коэффициент в начале координат; (R, γ) – элементы полярных координат точки; γ – полярный угол, зажатый между разверткой конуса, проходящей через точку, и развертки конуса, проходящей от центра предложения; R – длина развертки конуса, проходящей через точку; R0 – длина развертки конуса, проходящей от центра предложения; ε – продольное искажение в км.

И масштабный коэффициент, равный единице на расстоянии 174728 м от φ0 севера и юга. А это примерно приводит к тому, что масштабный коэффициент равен единице. То есть нет искажений при ширине 36,75° и 40,25°. А линейное искажение на широте, проходящей через центр системы, равно -37,44 см/км.

Формирование уравнения регрессии

Регрессионный анализ – это статистический метод анализа различных факторов и понимания того, какие из них могут повлиять на достижение цели, а какие можно игнорировать. В нашем случае его можно использовать для формирования уравнений регрессии геодезических координат от WGS84 до эллипса Кларка 1880, которые можно использовать вместо параметров преобразования [6].

Итоговый вывод показывает, насколько хорошо рассчитанное уравнение линейной регрессии соответствует вашему источнику данных.

R-квадрат – это коэффициент корреляции, который измеряет силу линейной зависимости между двумя переменными. Чем больше абсолютное значение, тем сильнее взаимосвязь.

− 1 означает прочные позитивные отношения;

− -1 означает сильную отрицательную связь;

− 0 означает отсутствие каких-либо отношений вообще.

Вычисление параметров преобразования (Leica_GEO_Office)

У нас есть шесть точек, распределенных вблизи района Пальмиры, который находится близко к центру сирийских координат, как видно на рис. 1. В табл. 1 показаны их местные координаты и с помощью GPS.

На рис. 2 показано геометрическое сжатие и начальные координаты системы координат Ламберта.

Используя четыре точки и с помощью метода Бурсы – Вольфа (семь параметров), мы вычисляем параметры перехода от WGS84 на Кларка 1880.

Локальные координаты и местные геодезические координаты (Кларк 1880) оставшихся двух точек, рассчитанные с использованием параметров преобразования, показанных в табл. 2.

Таблица 1

Геодезические и декартовы координаты точек

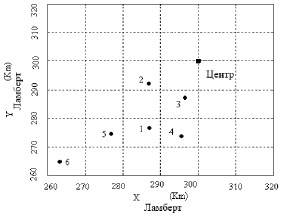
Рис. 1. Пункты геодезической сети

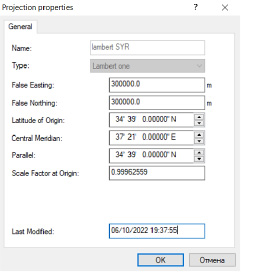
Рис. 2. Параметры системы координат Ламберта

Параметры перехода от WGS 84 на Кларка 1880 следующие:

− смещение по оси X TX = 758.2309 m;

− смещение по оси Y TY = -176.8499 m;

− смещение по оси Z TZ = 323.1733 m;

− поворот вокруг оси X RX'' = -6.82987'';

− поворот вокруг оси Y RY'' = -16.88788'';

− поворот вокруг оси Z RZ'' = -29.98073'';

− масштабный фактор S (PPM)= -98.6265 PPM.

Таблица 2

Декартовы координаты и местные геодезические координаты

Формирование уравнения регрессии геодезических координат от WGS84 до эллипса Кларка 1880 в Excel

Для формирования уравнения регрессии геодезических координат от WGS84 до эллипса Кларка 1880 были использованы четыре точки (табл. 3) и вычислены коэффициенты регрессии долготы и широты (табл. 4), и с использованием этих формул будут рассчитаны геодезические координаты оставшихся точек в локальном эллипсоиде Кларка 1880. Эти координаты указаны ниже в табл. 5.

Таблица 3

Геодезические координаты точек с географическими разностями координат

Таблица 4

Коэффициенты регрессии долготы и широты

И уравнение регрессии для геодезических координат от 84-й рабочей группы до эллипса Кларка 1880 г. будет выглядеть следующим образом:

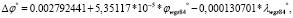
φКларк 1880,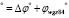

,

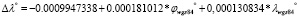λКларк 1880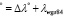

Таблица 5

Рассчитанные геодезические координаты

Таблица 6

Локальные различия в координатах

Таблица 7

Различия геодезических координат

Результаты исследования и их обсуждение

Сличая локальные координаты, рассчитанные с использованием программы Leica_GEO_Office, с известными координатами, мы обнажаем следующие разницы (табл. 6).

Сличая местные геодезические координаты, рассчитанные с использованием уравнений регрессии, и координаты, рассчитанные с использованием программы Leica_GEO_Office, мы обнажаем следующие разницы (табл. 7).

Из результатов сличения мы замечаем следующее:

– Разницы между вычисленными локальными координатами и известными не превосходят 0,53 м, мы замечаем, что результаты находятся в допустимых пределах, и поэтому параметры преобразования, рассчитанные с помощью программы Leica_GEO_Office, могут быть использованы для преобразования измеренных координат в локальные координаты.

− Различия между геодезическими координатами, рассчитанными с помощью программы Leica_GEO_Office, и координатами, полученными из уравнений регрессии, не превышают 0,004 с, и поэтому уравнения регрессии можно использовать для преобразования геодезических координат, измеренных с помощью GPS, в геодезические координаты на эллипсе Кларка 1880, и мы преобразуем геодезические координаты в прямоугольные координаты в системе Ламберта с использованием уравнений преобразования.

− Для получения высокой точности при преобразовании координат предпочтительно вычислять параметры преобразования или коэффициенты регрессии для каждого региона отдельно.

Заключение

На основе результатов анализа были рассмотрены современное состояние системы координат Ламберта в Сирийской Арабской Республике и вычисление параметров преобразования с использованием программного обеспечения Leica_GEO_Office и определение уравнения регрессии в Excel для преобразования геодезических координат, измеренных с помощью GPS, в геодезические координаты на эллипсе Кларка 1880 в Сирии.

Эта система использовалась в Сирийской Арабской Республике с 1920-х гг. и была принята до 1958 г. в качестве основы для создания карт сирийских земель Военно-геодезическим управлением. Основываясь на результатах предыдущего анализа, мы можем использовать эту проекцию для обновления сирийской геодезической сети, чтобы после войны сделать реконструкцию страны.