Проблема уравнивания геодезических построений является весьма важной процедурой при выполнении высокоточных геодезических измерений и обработке их результатов как в процессе создания опорных геодезических сетей, так и при выполнении точных и высокоточных геодезических работ, выполняемых в составе специальных инженерных изысканий при проектировании прецизионных сооружений и эксплуатации объектов горнодобывающей промышленности. Так, в местах строительства прецизионных сооружений линейного типа, к которым относятся строительно-технологические комплексы линейных ускорителей заряженных частиц, промышленные конвейеры тонких технологий и другие высокотехнологические объекты, создаются точные и высокоточные геодезические построения, обеспечивающие проведение высокоточных и инженерно-геодезических наблюдений. Фигурами таких построений могут быть: цепочки триангуляции и трилатерации, полигонометрические ходы и системы полигонометрических ходов, а также нивелирные ходы, системы нивелирных ходов и цепочек из нивелирных квадратов. Результаты геодезических измерений, в частности высокоточных нивелирований по цепочкам сдвоенных квадратов уравниваний, решают три основные задачи [1, 2]: определение по результатам геодезических измерений надежных значений искомых величин, а также их функций как косвенных результатов измерений оценки точности результатов измерений; оценки точности результатов измерений и функций измеренных величин.
В связи с тем, что устойчивость прецизионного сооружения прямо зависит от микродеформаций горных пород его основания [3, 4], возникает необходимость в исследовании видов таких микродеформаций и их кинематических характеристик. При этом постановка таких исследований предусматривает построение сетей высокоточного нивелирования, конфигурация которых привязана к геометрии сооружения. Так, для прямолинейного прецизионного сооружения (линейные ускорители, интерферометры, промышленные конвейеры тонких технологий и другие) создаются нивелирные сети в виде цепочек квадратов, в частности сдвоенных нивелирных квадратов (рисунок). Порядок обработки результатов высокоточного нивелирования по квадратам предусматривает уравнивание и оценку точности результатов нивелирования.
Основной целью исследования является разработка строгого способа оценки точности результатов нивелирования по квадратам.
Материалы и методы исследования
В соответствии с методом наименьших квадратов может быть вычислена общая формула обратного веса функции уравненных величин для сдвоенных нивелирных рядов из квадратов. Согласно данным о направлениях превышений по звеньям, приведенным на рисунке, условные уравнения поправок для сдвоенных рядов нивелирных квадратов можно предоставить в указанном виде:
I – верхний ряд нивелирных квадратов
(5i) + (5i – 1) + (5i – 2) – (5i – 6) + W2i-1 = 0, (1)
II – нижний ряд нивелирных квадратов
(5i) + (5i – 1) + (5i – 2) – (5i – 3) + W2i = 0, (2)
при текущем номере i от 1 до n.
Уравнивание приращений весовой функции [1] отметки конечной точки K или приращения по нивелирному ходу O-K (O – начальная точка) может быть представлена как 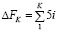 при i от 1 до K.
при i от 1 до K.
Коэффициенты нормальных уравнений для сдвоенных нивелирных рядов из одинаковых квадратов представляют собой пятидиагональную матрицу и определяются равенствами
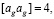 при g от 1 до 2n
при g от 1 до 2n
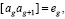 при g= 1 и g = 2n – 1 (3)
при g= 1 и g = 2n – 1 (3)
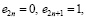
или
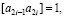 при i от 1 до n (4)
при i от 1 до n (4)
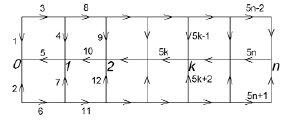
Схема сети из сдвоенных нивелирных квадратов
Далее:
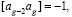 при g = 3, 4, …, 2n
при g = 3, 4, …, 2n
и 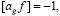 при g = 1, 1, …, 2K (5)
при g = 1, 1, …, 2K (5)
Откуда следует, что [ f f ] = K.
Тогда ошибка уравненной отметки точки равна
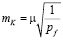 при
при 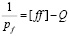 , (6)
, (6)
где μ – ошибка единицы веса, измеренного превышения стороны квадрата, Q – весовая функция.
Результаты исследования и их обсуждение
Одной из важных задач уравнительных вычислений в отношении нивелирного ряда из сдвоенных квадратов является оценка влияния уравнивания за условия полигонов на обратный вес любого элемента.
Общеизвестно [5–7], что составляющая обратного веса Q, как матрица весовых коэффициентов, определяется равенством
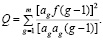 (7)
(7)
Раскрывая по общему правилу [1, 8] алгоритмы преобразованных нормальных уравнений, соответствующих условиям полигонов с учетом равенств (3) и (5), в которых [ah ag+1] при h = 1, 2, … (g – 2) имеет вид
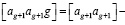
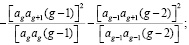 (8)
(8)
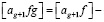
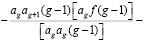
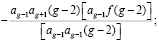 (9)
(9)
С учетом значений (1) и (2), получаем
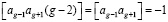
при g = 2, 3, … , 2n+1, (10)
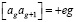 при g = 1, 2, … , 2n-1, (11)
при g = 1, 2, … , 2n-1, (11)
е2i+1 = eнечетн = 1 и е2i = eчетн = 0. (12)
Значение квадратичных членов преобразованных нормальных уравнений коррелат можно представить в виде простых дробей, что убедительно подтверждается в работе, а именно:
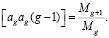 (13)
(13)
Так как при раскрытии алгоритмов имеем
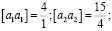
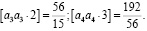
С учетом условных уравнений поправок (1), а также равенств (3), (4) и (13) после введения обозначений
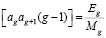 (14)
(14)
получим
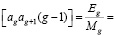
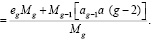 (15)
(15)
Тогда, с учетом (14) и (15), справедливо равенство
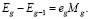 (16)
(16)
При E0 = 0 сумма равенств (16) если h = 1, 2, …, g реализуется в виде аналитического выражения
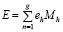 , где h = 1, 2, …, g. (17)
, где h = 1, 2, …, g. (17)
Далее, подставляя в (8) значения (13), (10) и (14) соответствующих алгоритмов, получим в общем виде
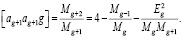 (18)
(18)
Из последнего равенства после его преобразования получаем
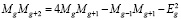 . (19)
. (19)
Из равенства (19), но с увеличенным на единицу индексом g, приняв во внимание (16), после сокращения на Mg+1, получим основную формулу для последовательного вычисления целых чисел M:
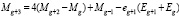 (20)
(20)
Равенство (20) при условиях (12) и (17) является рекуррентным уравнением для чисел М, служащих для получения квадратичных членов по формуле (13).
Подставляя в (9) выражения преобразованных и представленных формулами (18), (14) и (10) алгоритмов после сокращений (g+1)-го члена, получим
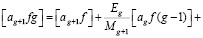
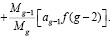 (21)
(21)
Выражая числа 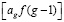 в виде простых дробей:
в виде простых дробей:
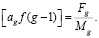 (22)
(22)
Из равенства (21) получим формулу для последовательного вычисления значений F:
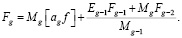 (23)
(23)
Используя равенства (18) и (22), найдем для любого члена формулы
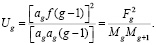 (24)
(24)
Рассмотрим последовательные значения сумм Sm:
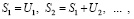
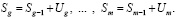 (25)
(25)
Величины Sg можно представить в виде простых дробей, знаменателями которых будут служить числа М, а числителями – новая последовательность целых чисел S:
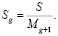 (26)
(26)
Подставляя в общий член последовательности (25) выражения для Sg, Sg-1 и Ug согласно формулам (24) и (26), получим формулу для вычисления каждого последующего значения Sg через предыдущие Sg-1 и числа M и F:
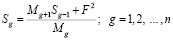 . (27)
. (27)
По формуле (27) можно последовательно вычислить Sg, начиная с S1, (положив S0 = 0) и заканчивая Sm.
При вычислении Sm получим величину Q, вносимую в обратный вес любого нивелирного ряда условными уравнениями полигонов [9]:
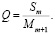 (28)
(28)
Последовательно подставляя F1, F2, … в виде разложения по коэффициентам 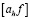 :
:
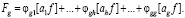 (29)
(29)
Согласно формуле (29) для вычисления чисел Fg необходимо соединить коэффициенты при 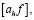 содержащиеся в разложениях Fg-1 и Fg-2, что позволяет записать следующее аналитическое выражение для вычисления чисел
содержащиеся в разложениях Fg-1 и Fg-2, что позволяет записать следующее аналитическое выражение для вычисления чисел 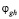 , а именно:
, а именно:
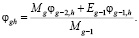 (30)
(30)
Следует показать, что если значения чисел 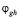 в таблице, в которой g – номер строки, а h – номер столбца, то последовательность чисел
в таблице, в которой g – номер строки, а h – номер столбца, то последовательность чисел 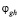 по столбцам и строкам удовлетворяют соответственно следующим двум возвратным уравнениям 4-го порядка с периодическими меняющимися коэффициентами е:
по столбцам и строкам удовлетворяют соответственно следующим двум возвратным уравнениям 4-го порядка с периодическими меняющимися коэффициентами е:
– для h-го столбца:
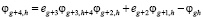 ,
,
при 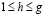 . (31)
. (31)
– для g-й строки:
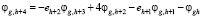 ,
,
при 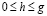 . (32)
. (32)
Начальными членами для φ будут два числа: 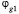 ,
, 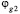 (полагая предшествующие числа равными нулю), а числа е определяются равенствами (12).
(полагая предшествующие числа равными нулю), а числа е определяются равенствами (12).
Значения коэффициентов 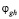
|
g |
Eg |
Mg |
Значения φ при различных h |
||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|||
|
1 |
1 |
1 |
1 |
||||||
|
2 |
1 |
4 |
1 |
4 |
|||||
|
3 |
16 |
15 |
4 |
1 |
15 |
||||
|
4 |
16 |
56 |
8 |
16 |
16 |
56 |
|||
|
5 |
208 |
192 |
16 |
8 |
56 |
16 |
192 |
||
|
6 |
208 |
712 |
47 |
68 |
120 |
225 |
208 |
712 |
|
|
7 |
2623 |
2415 |
68 |
47 |
225 |
120 |
712 |
208 |
2415 |
Аналогично разложению Fg используем формулы (27) и (29) для последовательного получения S в виде разложения по произведениям 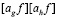 :
:
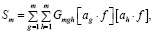 (33)
(33)
причем для последовательного вычисления G получим
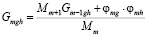 . (34)
. (34)
Величины G, как и M, E, φ, являются целыми положительными числами и определяются возвратным уравнением
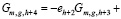
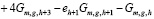 ,
,
при 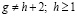 . (35)
. (35)
Из сопоставления формул (33) и (35) видно, что 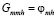 .
.
Подставив в это выражение 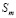 с учетом обозначения,
с учетом обозначения, 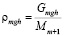 получим в окончательном виде формулу для вычисления величины любой весовой функции [9, 10]:
получим в окончательном виде формулу для вычисления величины любой весовой функции [9, 10]:
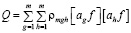 . (36)
. (36)
Заключение
В результате проведенных теоретических исследований рассмотрены вопросы оценки точности функции уравненных неизвестных. Получена общая формула обратного веса функции уравненных величин для нивелирного ряда из сдвоенных квадратов.



