Ионы тяжелых металлов, содержащиеся в сточных водах, являются ядовитыми компонентами для всех живых существ [1]. Такие ионы можно обнаружить в промышленных сточных водах различных производств. Среди тяжелых металлов свинец выделяется тем, что даже малое его содержание является высокотоксичным [2]. Накопление свинца в природной среде обусловлено наличием тетраэтилсвинца в автомобильном топливе, а также выбросами на ТЭЦ при сжигании угля. Аккумуляторные заводы являются главными потребители свинца. Более половины добываемого свинца используется для изготовления аккумуляторных батарей [3]. Гальванический процесс благополучно протекает в основном только с металлическим свинцом, кроме того, устойчивость против коррозии увеличивает эксплуатацию аккумуляторных батарей. Для удаления токсичных тяжелых металлов используется ряд различных технологий [4-6]. В настоящее время для извлечения тяжелых металлов из промышленных сточных вод увеличилось применение метода ионного обмена с использованием природных (минеральные) сорбентов [7-9].
Целью работы является оценка возможности извлечения свинца (II) из водных растворов диатомитом с возможным применением исследуемого сорбента для водоочистки.
Материал и методы исследования
Для извлечения ионов свинца был использован природный диатомит тонкодисперсный светло-серого цвета. Месторождение исследуемого диатомита – г. Ирбит Свердловской области. Основным компонентом химического состава диатомита является SiO2, кроме того минерал содержит оксиды алюминия, железа, магния и другие [10]. Химический состав исследуемого минерала представлен на рисунке 1. Точность определения ±2%. Анализ проведен с помощью сканирующей электронной микроскопии.
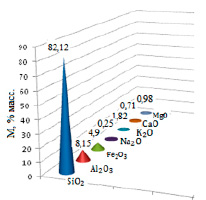
Рис. 1. Химический состав природного диатомита
Исследование сорбционной активности диатомита проводили в положении статики на модельных растворах с различной концентрацией катионов свинца. Для построения изотерм использовали модель Ленгмюра и Фрейндлиха. Исследования проводились в температурном режиме 298, 318 и 333 К. Для повышения количества поверхностных адсорбционных центров осуществляли обработку изучаемого минерала растворами HCl, NaOH и NaCl. В результате были получены Н-, ОН- и Na-разновидности исследуемого сорбента.
Результаты исследования и их обсуждение
Сорбционная активность диатомита вызвана взаимодействием гидроксильных групп глинистого минерала с катионами свинца. Поглощающая способность диатомита связана с реакционной активностью силановых групп и их численностью, что определяется степенью гидратации кремнезема. Описание процесса сорбции можно провести на основе построения изотерм. Вид изотермы характеризует меру сродства исследуемого сорбента к извлекаемым ионам. Кроме того на основе изотермы можно определить максимальную сорбционную способность исследуемого минерала. Количественным параметром сорбционного процесса является удельная сорбция (Г), которую вычисляли по формуле:
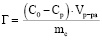 ,
,
где С0 – начальная концентрация ионов свинца в модельном растворе, моль/л;
Ср – равновесная концентрация ионов свинца, моль/л;
Vр-ра – объем исследуемого раствора, мл;
mc – масса исследуемого сорбента, г.
На рисунке 2 показаны изотермы, полученные при сорбции свинца на природном диатомите в различных температурных режимах.
Рисунок 2 демонстрирует, что с увеличением равновесной концентрации ионов свинца в растворе и температуры удельная сорбция увеличивается. При температуре 298 К величина сорбции составила 0,52 моль/г, при 318 К – 0,56 моль/г, при 333 К – 0,64 моль/г. На начальных участках полученных изотерм наблюдается резкий подъем, что доказывает сорбционное сродство природной формы диатомита к ионам свинца. Рисунок 3 показывает изотермы, полученные при сорбции свинца на различных разновидностях минерала.
Объяснить сорбционный процесс можно на основе моделей Ленгмюра и Фрейндлиха [11]:
1) модель Ленгмюра
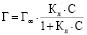 ,
,
или в линейной форме:
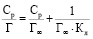 ,
,
где Г – величина удельной сорбции, моль/г;
Г∞ – величина предельной сорбции, моль/г;
Ср – равновесная концентрация свинца, моль/л;
Кл – константа равновесия сорбционного процесса.
2) модель Френдлиха
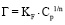 ,
,
или в линейной форме:
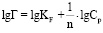
где КF ; n – константы Фрейндлиха.
Изотермы Ленгмюра – это теоретическая модель, которая представляет сорбцию как однослойную на однородной поверхности. Для описания процесса сорбции на разнородной поверхности сорбента можно использовать модель Фрейндлиха. Относительная сорбционная способность в уравнении Фрейндлиха определяется константой КF . Константа n характеризует интенсивность сорбционного процесса и распределение центров активности.
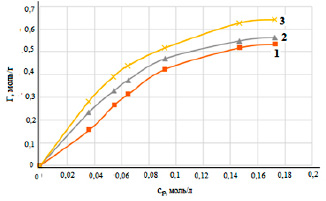
Рис. 2. Изотермы сорбции свинца на природном диатомите при температурах, К: 298(1), 313 (2), 333 (3)
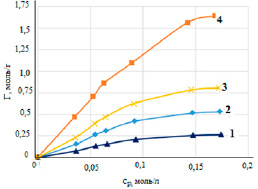
Рис. 3. Изотермы сорбции свинца на различных модификациях диатомита: Н-форма (1), природная форма (2), Na-форма (3), ОН-форма (4) при температуре 298 К
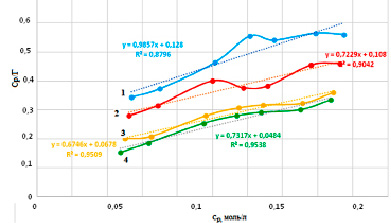
Рис. 4. Сорбционные изотермы свинца по уравнению Ленгмюра линейного вида для разных модификаций сорбента: 1-Н-форма, 2-природная форма, 3- Na-форма, 4- ОН-форма
Таблица 1
Постоянные уравнения Ленгмюра для различных форм диатомита
|
T, К |
Постоянные Ленгмюра |
|||||
|
Нативная форма |
ОН-форма |
|||||
|
Г∞, моль/г |
Кл |
R2 |
Г∞, моль/г |
Кл |
R2 |
|
|
298 |
1,18 |
0,210 |
0,9042 |
3,15 |
0,297 |
0,9538 |
|
318 |
1,96 |
0,089 |
0,9282 |
6,1 |
0,086 |
0,9787 |
|
333 |
2,4 |
0,079 |
0,9512 |
7,84 |
0,072 |
0,9975 |
|
T, К |
H-форма |
Na-форма |
||||
|
Г∞, моль/г |
Кл |
R2 |
Г∞, моль/г |
Кл |
R2 |
|
|
298 |
0,58 |
0,214 |
0,8796 |
1,75 |
0,22 |
0,9509 |
|
318 |
0,96 |
0,09 |
0,8845 |
2,97 |
0,088 |
0,9651 |
|
333 |
1,15 |
0,086 |
0,9264 |
3,77 |
0,074 |
0,9852 |
Если n равняется 1, это означает, что все сорбционные центры одинаковы по величине.
Когда n оказывается больше 1, энергетическая связь сорбента и сорбтива уменьшается в процессе заполнения всей поверхности сорбента. В том случае, когда величина n имеет значение меньше 1, энергия связи будет увеличиваться и тогда сначала заполняются сорбционные центры с меньшей энергией [11].
Для вычисления констант уравнения Ленгмюра строили графическую зависимость в координатах Ср / Г – Ср, представленную на рисунке 4.
Постоянные Ленгмюра для всех форм сорбента приведены в таблице 1.
Результаты, представленные в таблице 1 показывают, что ОН-модификация диатомита является более благоприятной по отношению к катионам свинца. В этой модифицированной форме величина удельной сорбция имеет наибольшие значения.
Для определения констант уравнения Фрейндлиха были построены графики зависимости в координатах lgГ– lgCp, изображенные на рисунке 5.
Постоянные Фрейндлиха для всех форм диатомита приведены в таблице 2.
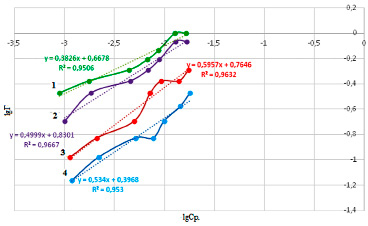
Рис.5. Изотермы сорбции свинца в координатах линейного вида уравнения Фрейндлиха в разных формах сорбента: 1-ОН-форма, 2- Na -форма, 3- природная форма, 4- Н- форма
Таблица 2
Постоянные уравнения Фрейндлиха для различных форм диатомита
|
T, К |
Постоянные Фрейндлиха |
|||||
|
Нативная форма |
ОН-форма |
|||||
|
n |
КF |
R2 |
n |
КF |
R2 |
|
|
298 |
0,66 |
1,06 |
0,9632 |
2,71 |
1,97 |
0,9506 |
|
318 |
0,74 |
2,1 |
0,9748 |
30,86 |
3,34 |
0,9798 |
|
333 |
0,92 |
2,2 |
0,9885 |
181,8 |
3,38 |
0,9898 |
|
T, К |
H-форма |
Na-форма |
||||
|
n |
КF |
R2 |
n |
КF |
R2 |
|
|
298 |
1,25 |
0,46 |
0,953 |
2,7 |
0,49 |
0,9667 |
|
318 |
1,54 |
0,059 |
0,9722 |
1,33 |
1,37 |
0,9793 |
|
333 |
2,37 |
0,011 |
0,9931 |
1,4 |
1,43 |
0,9816 |
Результаты, представленные в таблице 2 показывают, что постоянная Фрейндлиха n имеет значение больше 1 для всех модифицированных форм диатомита, а значит все эти формы являются выгодными для извлечения ионов свинца. Более выгодным является ОН-модификация диатомита. Величина постоянной Фрейндлиха КF свидетельствует о свободном перемещении ионов свинца из раствора в фазу сорбента и сорбционной активности ОН-формы диатомита к извлекаемым ионам свинца.
Выводы
На основании полученных результатов можно сделать следующие выводы.
1. Исследованный природный минерал (диатомит) проявляет сорбционную способность к извлекаемым ионам свинца, поэтому его можно использовать в целях водоочистки.
2. Химическое модифицирование поверхности сорбента позволило повысить сорбционные характеристика диатомита. Наибольшее количество активных центров имеет диатомит при щелочной модификации.



