Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

В настоящей работе обсуждается задача формирования фильтра, основанного на различии фазовых свойств измеряемого сигнала и искажающей его помехи. Фаза измеряемого сигнала предполагается регулярной, а фаза шума - случайная функция.

Как было показано ранее [1], подобный фильтр может быть построен с использованием опорного импульса специального вида, показанного на рис. 1.

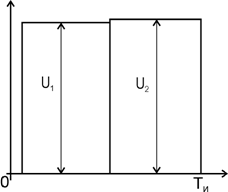
Рис. 1. Форма опорного импульса

Импульс имеет две прямоугольные ступени с амплитудами U₁ и U₂ соответственно, общая длительность ступеней немного меньше длительности интервала наблюдения Т_И.

Как показали результаты анализа, при соотношениях амплитуд ступеней сигнала и отношении длительности интервала измерения к общей длительности ступеней близких к 1 увеличивается чувствительность фазы к изменению напряжения (амплитуды ступени U₂). При этом зависимость фазы от D (отношение амплитуды второй ступени к амплитуде первой) M (отношение длительности интервала измерения к суммарной длительности ступеней) имеет вид:

На рис. 2 показан график зависимости фазы основной гармоники спектра импульсного сигнала с частотой w от D при значении M=1.000500025. Как видно из рисунка, при переходе этого отношения через 1 в интервале значений D от 0.9999 до 1.0001 значение фазы изменяется скачком, а при дальнейшем удалении от 1 асимптотически приближается для малых значений к -p/2 а для больших к p/2.

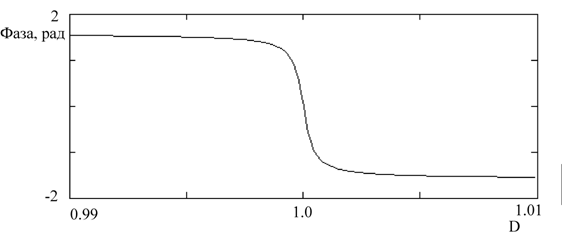
Рис. 2. График зависимости фазы основной гармоники опорного сигнала
от отношения амплитуд первой и второй ступеней при значении M=1.000500025

Если на интервале от Т_И/2 до Т_И у опорного импульса появится случайная помеха, то его гармоническая составляющая w_i будет модулирована по амплитуде и фазе в виде:

.

Это колебание может быть представлено в виде разложения при условии ограничения амплитуды:

,

где J_n(b) - функция Бесселя n-го порядка от аргумента b. В данном случае, аргумент функции Бесселя (глубина модуляции) равен , где Ω - значение частоты основной гармоники, а φ_n - значение фазы модулирующего сигнала.

Если модулирующих синусоидальных составляющих несколько, то получим [2]:

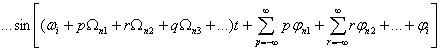,         (1)

где β - глубины модуляции, Ω - частоты, а φ - начальные фазы модулирующих гармоник. Учитывая взаимное уничтожение членов нечетных порядков J_n(β)_, в сумму входят члены только четных порядков. Таким образом, модулируемое колебание содержит набор частот, отстоящих выше и ниже от основной частоты. Учитывая, что при модуляции полная энергия колебания не меняется, появление комбинационных частот приводит к уменьшению энергии основной частоты и перераспределению ее на другие частоты. Этот фактор определяет эффективность фильтра. Хотя в выражении (1) оператор суммирования выполняется для индексов от минус бесконечности до плюс бесконечности, в реальных вычислениях, в силу быстрого убывания значений функции Бесселя высоких порядков и учитывая только слагаемые по модулю больше 0.01, для суммирования достаточно трех членов 0, 2, 4 порядка.

Другим важным параметром, определяющим эффективность описываемого фильтра, является глубина модуляции. Анализ показывает, что если при появлении помехи знак разности 1- D не меняется, то максимальная глубина фазовой модуляции не больше, чем p/2 (гармоники находятся в противофазе). Фактически достижима даже меньшая глубина модуляции. Для такого аргумента значение функции Бесселя нулевого порядка будет больше значений этой функции для более высоких порядков, а следовательно, среди комбинаторных частот, получающихся при фазовой модуляции в соответствии с выражением (1) значение амплитуды основной частоты будет максимальным. В табл. 1 приведены значения амплитуд комбинаторных частот при фазовой модуляции четырьмя гармониками. На рис.3 приведен график распределения этих амплитуд.

Таблица 1

Распределение амплитуд для комбинаторных частот при фазовой модуляции сигнала на основной частоте, равной 1. Модулирующие гармоники имели частоты 0.01, 0.02, 0.03 и 0.04, глубина модуляции 1.57

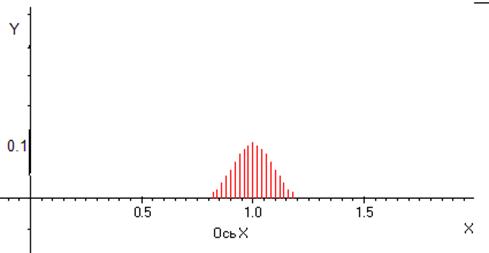
Рис. 3. Распределение амплитуд комбинаторных частот при фазовой модуляции сигнала
на основной частоте, равной 1. Частоты модулирующих гармоник равны 0.01, 0.02, 0.03 и 0.04, глубина модуляции 1.57

Как видно из рис. 3, максимальной амплитуде является гармоника на основной частоте 1. При увеличении глубины модуляции можно получить существенное уменьшение амплитуды основной гармоники по сравнению с комбинаторными. В табл. 2 приведены значения амплитуд комбинаторных гармоник при глубине модуляции, равной 2.5, а на рис.4 приведен график распределения амплитуд для этого случая.

Таблица 2

Распределение амплитуд для комбинаторных частот при фазовой модуляции сигнала на основной частоте, равной 1. Модулирующие гармоники имели частоты 0.01, 0.02, 0.03 и 0.04, глубина модуляции 2.5

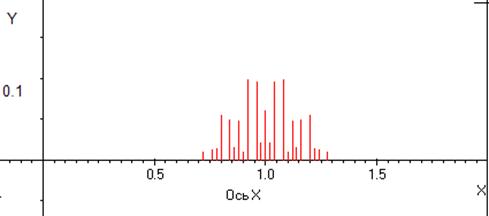
Рис. 4. Распределение амплитуд комбинаторных частот при фазовой модуляции сигнала
на основной частоте, равной 1. Частоты модулирующих гармоник равны 0.01, 0.02, 0.03 и 0.04, глубина модуляции 2.5

Для случайных чисел, равномерно распределенных на исследуемом интервале с математическим ожиданием 0.01 значение фазы основной гармоники оказалось равным 0.4529350452. Таким образом, достигнута глубина модуляции порядка 2.1. Как видно из анализа рис.2, для достижения глубины модуляции больше чем p/2 необходимо, чтобы при появлении помехи знак разности 1- D изменился. Для этого необходимо, чтобы для опорного импульса D<1, а появление помехи приводило к D>1.

Так при модельных вычисления для опорного импульса с параметрами D=0.999900 и M=1.000500025 значение фазы основной гармоники было равно -1.56766724, а при появлении помехи, состоящей из гармоники с частотой 0.05 от основной и амплитудой 0.02, а также последовательности.

СПИСОК ЛИТЕРАТУРЫ

1. Патент 2133474 Россия. МКИ 19/02. Способ измерения сигналов произвольной формы в присутствии случайных шумов/ Д.К.Авдеева. заявлено 30.10.1997; Опубл. 20.07.1997, Бюл. № 20.15с.
2. Гоноровский И.С. Радиотехнические цепи и сигналы: учебник для ВУЗов.- 4-е изд.; М.: «Радио и связь», 1986. - 512 с.