Одной из актуальных проблем при проектировании оборудования в химической является разделение жидкости со значительным содержанием абразивных твердых частиц.
Рассматривается задача об ударном взаимодействии потока суспензии с наклонной неподвижной поверхностью. Расчетная схема представлена на рис.1
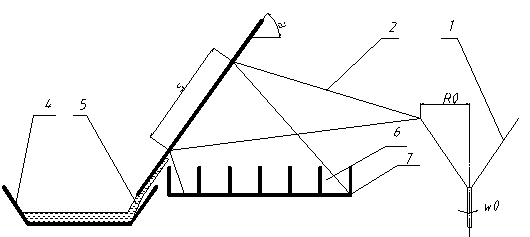
Рисунок 1. Расчетная схема
Конический распылитель 1 подает поток 2 на наклонный отбойник 3, После удара суспензии происходит ее разделение. Осветленная фаза 5, состоящая из жидкой фазы с увлекаемыми ею твердыми частицами, которые не смогли преодолеть поверхностного натяжения жидкого слоя и вырваться из ее потока. Сгущенная фаза 6, состоящая из отраженного потока наиболее крупных твердых частиц и капель жидкой фазы.
Наличие случайных факторов в процессе описанного ударного взаимодействия требуют вероятностного подхода к решению задачи.
Фазовое пространство для системы частиц потока суспензии определяется совокупностью одной компоненты скорости центра масс частицы и ее диаметра[1]. Распределение числа частиц осветленной фракции dN в элементе фазового объема экспоненциально зависит от стохастической энергии частицы Е [2].
![]() (1)
(1)
![]() , (2)
, (2)
![]() (3),
(3),
где ![]() ─ плотность твердых частиц,
─ плотность твердых частиц, ![]() ─ вязкость жидкости,
─ вязкость жидкости,![]() ─ угловая скорость распылителя, R─ расстояние от оси вращения до отбойника, k ─ коэффициент пропорциональности.
─ угловая скорость распылителя, R─ расстояние от оси вращения до отбойника, k ─ коэффициент пропорциональности.
Параметр А в выражении (1) определяется из условия нормировки
![]() (4)
(4)
тогда при ![]()
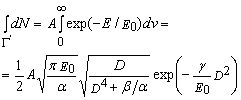 (5)
(5)
Вид дифференциальной функции распределения твердых частиц осветленной фракции по диаметрам следует из выражения(1)
![]() (6)
(6)
с учетом (6)
![]() (7)
(7)
отношения N/А определяются с помощью выражений (1),(3),(5)
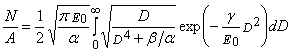 (8)
(8)
Число твердых частиц N находим из экспериментальных данных [4]
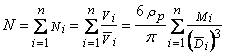 (9)
(9)
где
![]() (10)
(10)
n ─ число фракций, Ni и Vi ─ число твердых частиц и их объем в i-й фракции,![]() ─ объем частицы со средним диаметром
─ объем частицы со средним диаметром ![]() в i-й фракции, Мi ─ экспериментальная масса частиц в i-й фракции.
в i-й фракции, Мi ─ экспериментальная масса частиц в i-й фракции.
Параметр Е0, определяется из уравнения энергетического баланса.
![]() (11)
(11)
где Е0 ─ энергия налетающих твердых частиц, Е1 и Е2 ─ энергии твердых частиц осветленной и сгущенной фазы.
![]() (12)
(12)
 (13)
(13)
![]() (14)
(14)
где ![]() ,
, ![]()
![]() ─ скорость частиц налетающего факела суспензии,
─ скорость частиц налетающего факела суспензии,![]() ─ скорость осветленной фазы,
─ скорость осветленной фазы,![]() ─ скорость частиц отраженного потока i-й фракции, попадающих в j ячейку ловушки,
─ скорость частиц отраженного потока i-й фракции, попадающих в j ячейку ловушки, ![]() и
и ![]() ─ массы потоков налетающей и сгущенной суспензии,
─ массы потоков налетающей и сгущенной суспензии, ![]() ─ масса жидкости осветленной фазы, n ─ число ячеек ловушки.
─ масса жидкости осветленной фазы, n ─ число ячеек ловушки.
Скорость частиц i-й фракции сгущенной фазы ![]() может быть определена по экспериментальному значению коэффициента восстановления
может быть определена по экспериментальному значению коэффициента восстановления ![]() при ударе [4].
при ударе [4].
Вид функции распределения твердых частиц в осветленной фазе позволяет определить критическое значение диаметра частиц ![]() , соответствующее максимальному значению для функции распределения(8) и минимальному значению для функции распределения частиц в сгущенной фазе.
, соответствующее максимальному значению для функции распределения(8) и минимальному значению для функции распределения частиц в сгущенной фазе.
![]() , (16)
, (16)
![]() ,
,
 .
.
Коэффициент ![]() определяется из условия равенства экспериментального значения
определяется из условия равенства экспериментального значения ![]() дифференциального распределения частиц в потоке суспензии до удара при
дифференциального распределения частиц в потоке суспензии до удара при ![]()
 (17)
(17)
где

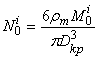 ,
, 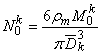 (18)
(18)
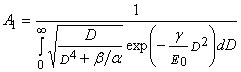 (19)
(19)
где ![]() и
и ![]() ─ числа частиц суспензии и их экспериментальная масса,
─ числа частиц суспензии и их экспериментальная масса, ![]() и
и ![]() ─ число частиц суспензии и их экспериментальная масса к-й фракции, соответствующей критическому значению диаметра
─ число частиц суспензии и их экспериментальная масса к-й фракции, соответствующей критическому значению диаметра ![]() .
.
Предложенная модель осветленной фазы суспензии получила экспериментальное подтверждение, и может быть использована для описания движения частиц сгущенной фазы после ударного взаимодействия суспензии.
СПИСОК ЛИТЕРАТУРЫ
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учебное пособие в 10 т. Т.VI. Гидродинамика. - М.: Наука. 1988.
- Зайцев А.И., Бытев Д.О. Ударные процессы в дисперсно-пленочных системах. - М.: Химия, 1994. 176с.
- Дьяконов В. Maple 6: учебный курс. СПб.: Питер, 2001.
- Ландау Л.Д., Лифшиц Е.М. Теоретическая физика: Учебное пособие в 10 т. Т.I. Механика. - М.: Наука. 1988.



