Scientific journal

Advances in current natural sciences

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

При выполнении имитационного моделирования процесса функционирования технических систем с использованием сетей Петри-Маркова (СПМ) [1] актуальной является задача хранения структуры и используемых сетей для ускорения их загрузки в память ЭВМ и оперирования их параметрами.

СПМ может быть представлена в виде множества

,

где  - конечное множество позиций,  - конечное множество переходов, N(a) - общее количество позиций, N(z) - общее количество переходов, O_A(Z) - выходная функция переходов [2].

В контексте задачи моделирования процесса отказов/восстановлений:

- позиции множества A = {(a₁, ..., a_i, ..., a_N(A)} являются математическим подобием состояний элементов системы;

- переходы множества Z = {z₁, ..., z_i, ..., z_N(Z)} моделируют взаимодействие элементов при переключениях системы из одного состояния в другое, при этом во временной области взаимодействие может рассматриваться как «соревнование» отказов/восстановлений, исходом которого является переключение системы в одно из возможных сопряженных состояний;

- выходная функция позиции О_Z(a_i) = {z_{1[О, N(z)]}, ..., z_{j[О, N(z)]}, ..., z_{N[О, N(z)]}} ⊂ Z моделирует множество состояний, участвующих в «соревновании», (N[O, N(a_j)] - общее количество переходов, составляющих выходную функцию O_Z(a_i) позиции a_i);

- выходная функция перехода О_А(z_i) = {а_{1[О, N(z)]}, ..., a_{j[О, N(z)]}, ..., a_{J[О, N(z)]}} ⊂ A моделирует множество исходов «соревнований» отказов/восстановлений элементов (N[О, N(z_j)] - общее количество позиций, составляющих выходную функцию О_А(z_j) перехода z_j).

Кроме того, каждый элемент рассматриваемого множества П характеризуется набором параметрических аспектов. Такой набор аспектов различен для позиций и переходов. Каждая позиция характеризуется следующим набором параметров:

,

где p_i - вероятность выполнения полушага в соответствующий переход,  - плотность распределения времени пребывания маркера в позиции.

Как показывает практика, наиболее часто используемыми законами распределения  являются законы Пуассона и Эрланга k-го порядка, поэтому для однозначной записи закона  достаточно параметра , определяющего интенсивность потока событий и параметра  - порядка закона распределения Эрланга.

Для переходов также существует множество параметров, которые определяют структуру СПМ:

,

где  - логическая переменная, обозначающая наличие или отсутствие «полушага» [2] в переход z_i из позиции a_k.

  С учетом сказанного выше определяется список параметров, которые необходимы для полного воспроизведения структуры СПМ:

1. множество символических имен позиций A;

2. множество символических имен переходов Z;

3. выходная функция позиций О_Z(.);

4. выходная функция переходов О_A(.);

5. множество параметрических аспектов позиций М(а);

6. множество логических переменных M(z).

  Удобным инструментом для хранения и оперирования подобными данными являются базы данных, таблицы в которых связаны между собой по первичному ключу.

Вычислим объем информации, который может потребоваться для хранения одной записи в таблицах, соответствующих обозначенным выше пунктам 1-6:

1. Объем информации, необходимый для хранения символьных имен позиций вычисляется следующим образом:

,

где  - объем информации, необходимый для хранения одного символа строки, обычно  байт;  - максимальная длина строки-имени позиции в символах, обычно ; i_k - объем информации, необходимый для хранения значения первичного ключа, обычно  байт.

2. Аналогичным образом вычисляется объем информации I_Z, необходимый для хранения символьных имен переходов.

.

3. Объем информации , требуемый для записи выходной функции переходов, составляет переменную величину и зависит от количества N[О, N(z_j)] - общее количество позиций, составляющих выходную функцию О_А(z_j) перехода z_j:

.

В данном случае  байт требуется для хранения первичных ключей записей таблицы, содержащей выходную функцию переходов. Еще  байт требуется для записи ключа перехода, относящегося к текущей записи таблицы. Далее, для каждой записи потребуется по  байт информации.

4. По аналогии рассчитывается объем информации  для хранения выходной функции позиций:

.

5. Для записи параметрических аспектов позиций  требуется использование

 байт,

где i_p - количество байт, необходимое для хранения числа с плавающей запятой. В данном случае  байт используется для хранения первичного ключа записи таблицы, содержащей параметрические аспекты позиции. Еще  байт содержат идентификаторы записей позиций,  байт содержат информацию о величине параметров  соответственно.

6. Запись параметрических аспектов переходов требует использование

 байт,

где  - число позиций, из которых осуществляется «полушаг» в переход z_i. Очевидно, что .

Таким образом, для хранения в базе данных информации о структуре сети Петри-Маркова необходимо использовать 6 таблиц. Структура таблиц для хранения символьных имен позиций / переходов (names_a / names_z) приведена ниже:

Рис. 1. Структура таблицы для хранения символьных имен

Для хранения выходных функций позиций целесообразно использовать таблицы следующей структуры (output_a):

Рис. 2. Структура таблицы для хранения выходной функции позиций

Список переходов представляет собой сериализованный массив идентификаторов переходов, в которые осуществляется «полушаг» из позиции, идентификатор которой записан в поле A_id текущей записи.

Для хранения выходной функции переходов используется таблица, использующая структуру, представленную ниже (output_z).

Рис. 3. Структура таблицы для хранения выходной функции переходов

По аналогии с предыдущей таблицей список позиций представляет собой сериализованный список идентификаторов позиций, в которые осуществляется «полушаг» из перехода, идентификатор которого записан в поле Z_id текущей записи.

Для хранения параметрических аспектов позиций используется следующая структура таблицы базы данных (params_a):

Рис. 4. Структура таблицы для хранения параметрических аспектов позиций

Структура таблицы (params_z), используемой для хранения множества логических переменных переходов, приведена ниже.

Рис. 5. Структура таблицы для хранения параметрических аспектов переходов

Список логических переменных представляет собой также сериализованный массив идентификаторов позиций, для которых текущий переход (Z_id) содержится во множестве О_Z(a_i) текущей позиции a_i. Объединение логических переменных осуществляется с использованием логической операции коньюнкции.

На рис. 6 показана общая структура связи описанных выше таблиц в базе данных.

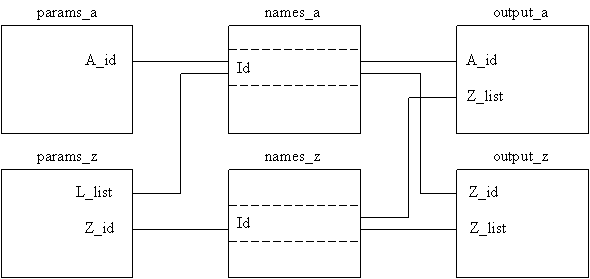
Рис. 6. Структура связей таблиц в базе данных

Таким образом, представленные в статье соотношения позволяют вычислить памяти ЭВМ, необходимый для хранения информации о структуре сети Петри-Маркова определенной структуры.

Работа выполнена при поддержке Российского фонда фундаментальных исследований.

СПИСОК ЛИТЕРАТУРЫ:

1. Ушаков И.А. Вероятностные модели надежности информационно-вычислительных систем. - М.: Радио и связь, 1991. - 132 с.
2. Ларкин Е.В., Сабо Ю.И. Применение сетей Петри-Маркова при моделировании структурных отказов в системе // Известия ТулГУ. Серия: Вычислительная техника. Информационные технологии. Системы управления. Т. 4. Вып. З. Системы управления. - Тула: ТулГУ, 2003. С.: 95 - 103.