Природа и характер информативных признаков, используемых при решении задач распознавания, могут быть самыми различными - спектральные плотности эталонных сигналов, автокорреляционные функции, средние значения и т.п. [1]. В том числе достаточно широко используются гистограммные оценки плотностей распределения вероятностей появления значений сигналов, не требующие значительных вычислительных затрат. В зависимости от физической природы сигнала такие оценки могут интерпретироваться по-разному. Например, в системах технического зрения, где в качестве первичного источника информации используются цифровые модели изображений, такие гистограммы характеризуют распределение вероятностей появления пикселей с заданным уровнем яркости, или, в многомерном случае, с заданным цветовым оттенком.
Оценка плотности распределения по гистограмме будет являться случайной величиной, распределение которой должно зависеть от объёма выборки отсчётов сигнала, по которой формируется эта оценка, а также, возможно, от ряда других факторов. Поэтому для принятия решения о целесообразности её использования как информативного признака, необходимо установить вид этого распределения и его основные параметры.
Пусть ![]() - сигнал, воспринимаемый ИИС, подвергшийся дискретизации и квантованию. Здесь η - Nd - мерный обобщённый аргумент, определяющий положение текущего отсчёта в сигнальной области (пространстве, времени, спектральной зоне и т.п.). Каждый отсчёт может принимать одно из конечного множества значений
- сигнал, воспринимаемый ИИС, подвергшийся дискретизации и квантованию. Здесь η - Nd - мерный обобщённый аргумент, определяющий положение текущего отсчёта в сигнальной области (пространстве, времени, спектральной зоне и т.п.). Каждый отсчёт может принимать одно из конечного множества значений ![]() , где n - число уровней квантования. Если исходный непрерывный сигнал описывался плотностью распределения
, где n - число уровней квантования. Если исходный непрерывный сигнал описывался плотностью распределения ![]() , то дискретная последовательность будет описываться рядом распределения
, то дискретная последовательность будет описываться рядом распределения ![]() .
.
Для вычисления локальной оценки этого ряда в некоторой точке ![]() , выделим в её окрестности область-апертуру заданных размеров и формы, по которой будет вычисляться гистограмма
, выделим в её окрестности область-апертуру заданных размеров и формы, по которой будет вычисляться гистограмма ![]() .
.
Пусть мощность множества отсчётов сигнала, ограниченных апертурой, равна N. Перенумеруем последовательно рассматриваемые отсчёты: ![]() . Элемент гистограммы hi по определению представляет собой частоту появления отсчётов со значением, равным xi, т.е.
. Элемент гистограммы hi по определению представляет собой частоту появления отсчётов со значением, равным xi, т.е. ![]() , где
, где ![]() - число отсчётов, равных
- число отсчётов, равных ![]() .
.
С ростом N частоты hi сходятся по вероятности к элементам ряда распределения ![]() , однако для любого конечного значения N величины hi будут являться случайными. Для принятия решения о целесообразности использования оценки H в задаче распознавания, необходимо выяснить характер и параметры законов распределения величин hi. Можно показать, что при рассмотрении некоррелированных сигналов, или использовании достаточно больших апертур распределение hi является биномиальным.
, однако для любого конечного значения N величины hi будут являться случайными. Для принятия решения о целесообразности использования оценки H в задаче распознавания, необходимо выяснить характер и параметры законов распределения величин hi. Можно показать, что при рассмотрении некоррелированных сигналов, или использовании достаточно больших апертур распределение hi является биномиальным.
Для доказательства рассмотрим процесс формирования величины hi. Анализ j-го отсчёта сигнала является случайным опытом с парой возможных исходов: попадание значения сигнала в i-ый уровень квантования с вероятностью ![]() , и непопадание с вероятностью
, и непопадание с вероятностью ![]() . Множество
. Множество ![]() можно интерпретировать как серию S, состоящую из N опытов принимающую один из 2N возможных исходов с вероятностями:
можно интерпретировать как серию S, состоящую из N опытов принимающую один из 2N возможных исходов с вероятностями:
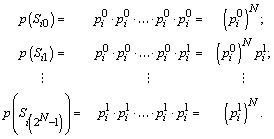
По аналогии с булевыми векторами будем называть весом серии Sik число ![]() , равное числу первых исходов в этой серии.
, равное числу первых исходов в этой серии.
Разобьём множество возможных исходов серий опытов ![]() на N+1 подмножество - группы серий {Gil}, l=0,K,N, элементы которых имеют равный вес. Вероятность появления любой серии Sik, принадлежащей группе Gil, будет равна
на N+1 подмножество - группы серий {Gil}, l=0,K,N, элементы которых имеют равный вес. Вероятность появления любой серии Sik, принадлежащей группе Gil, будет равна ![]() .
.
Число серий, относящихся к ![]() -ой группе, устанавливается из комбинаторных соображений, и равно числу сочетаний
-ой группе, устанавливается из комбинаторных соображений, и равно числу сочетаний ![]() . Таким образом, суммарная вероятность всех серий, принадлежащих группе
. Таким образом, суммарная вероятность всех серий, принадлежащих группе ![]() , описывается выражением:
, описывается выражением:
![]() .
.
Элемент hi, являющийся частотой появления отсчётов со значением xi, представляет собой дискретную случайную величину, принимающую одно из множества значений ![]() . Вес серии, отнесённый к её длине, имеет размерность частоты появления отсчёта xi, при этом p(Gil) представляет собой ни что иное, как искомый ряд распределения вероятностей
. Вес серии, отнесённый к её длине, имеет размерность частоты появления отсчёта xi, при этом p(Gil) представляет собой ни что иное, как искомый ряд распределения вероятностей ![]() , т.е.
, т.е.
![]() (1)
(1)
Таким образом, первоначальное утверждение о характере ряда распределения hi справедливо.
В отличие от схемы Бернулли при анализе гистограмм интерес представляют не абсолютные числа положительных исходов, а их относительные частоты ![]() . При этом несколько модифицируются выражения для математического ожидания
. При этом несколько модифицируются выражения для математического ожидания ![]() и дисперсии
и дисперсии ![]() .
.
В частности можно показать, что математическое ожидание найденного ряда распределения будет равно
![]() , (2)
, (2)
а дисперсия равна
![]() .(3)
.(3)
Зависимости (1-3) позволяют определить диапазон, в который будут попадать оценки плотности распределения ![]() по гистограмме H для заданного объёма выборки и априорных вероятностей появления значений сигнала. На рис. 1 показан пример разброса оценок при нормальном распределении
по гистограмме H для заданного объёма выборки и априорных вероятностей появления значений сигнала. На рис. 1 показан пример разброса оценок при нормальном распределении![]() .
.
Таким образом, при ограниченном размере апертуры элементы hi гистограммы будут распределены биномиально, а их математическое ожидание будет равно априорной вероятности появления в сигнале отсчётов со значением xi, т.е. ![]() . Дисперсия элементов hi убывает с ростом объёма выборки N, т.е. увеличение размеров апертуры делает оценку ряда
. Дисперсия элементов hi убывает с ростом объёма выборки N, т.е. увеличение размеров апертуры делает оценку ряда ![]() по гистограмме статистически более обоснованной. Найденные зависимости позволяют определить целесообразность использования гистограммных оценок при решении задачи распознавания.
по гистограмме статистически более обоснованной. Найденные зависимости позволяют определить целесообразность использования гистограммных оценок при решении задачи распознавания.
Литература
- Ларкин Е.В., Котов В.В. Особенности идентификации событий методами вейвлет-анализа. // Известия Тульского государственного университета. Серия: Математика. Механика. Информатика. Том 7. Вып. 3. Информатика - Тула: изд-во ТулГУ, 2001. - 200 с. (С. 96-103)
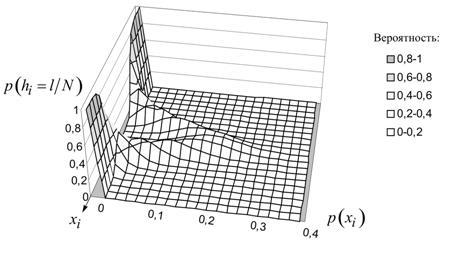
Рис. 1. Пример разброса гистограммных оценок при нормальном распределении значений сигнала
Библиографическая ссылка
Котов В.В. ИСПОЛЬЗОВАНИЕ ГИСТОГРАММНЫХ ОЦЕНОК В ЗАДАЧАХ РАСПОЗНАВАНИЯ // Успехи современного естествознания. 2004. № 4. С. 40-42;URL: https://natural-sciences.ru/ru/article/view?id=12473 (дата обращения: 09.03.2026).



