Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Файлы

Ферзалиев А. С.

Статья в формате PDF

123 KB

1. В работе вводятся проективно - точечные и проективно - плоские пространства гиперплоскостных элементов с кручениями. Пусть  является пространством гиперплоскостных элементов с формой связности , где - объект аффинной связности, - тензор, . В  рассмотрим аффинные  - пути (обобщенные геодезические кривые), определяемые следующими дифференциальными уравнениями 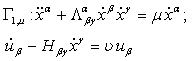[1]

 ,                              (1)

где , , , , .

Пространство гиперплоскостных элементов с объектом аффинной связности  с кручением, зависящей только от координат точки  обозначим через , где ,  ,  .

В пространстве  рассмотрим аффинные - пути

.            (2)

Определение 1. Пространство гиперплоскостных элементов  с кручением назовем проективно - точечным или  - пространством, если оно допускает геодезическое отображение на пространство  с кручением.

Из этого определения следует, что аффинные  - пути (1) переходят (отображаются) в аффинные - пути (2). Тогда связность пространства  характеризуется следующими основными уравнениями:

 ; ;  .                   (3)

Связность (3) приводит к следующим тензорам кривизны :

 , (4)

 ,                                    (5)

 ,                         (6)

где введены тензоры:

, (7)

,           (8)

,           (9)

.           (10)

В (7) ковариантное дифференцирование первого типа ,, , " ведется в симметрированной связности  , а в (8) - в связности  с кручением.

Из (4) - (6) исключив ,  ,  получим следующие равенства:

 , ,         (11)

и тензоры проективной кривизны

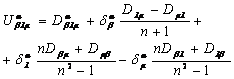,               (12)

,           (13)

            (14),

где  - тензор Г. Вейля проективной кривизны, отнесенный к связности  без кручения; тензор  имеет структуру , причем,  - тензоры кривизны обычного точечного пространства аффинной связности  с кручением,  - тензор кривизны связности .

2. Пусть  является плоским пространством гиперплоскостных элементов. Аффинные пути плоского пространства характеризуются следующими дифференциальными уравнениями

 ;  .             (13)

Определение 2. Пространство гиперплоскостных элементов  с кручением назовем проективно-плоским или  - пространством, если оно допускает геодезическое отображение на плоское пространство  .

Аффинные пути (1) пространства  отображаются в аффинные пути (13) плоского пространства . Тогда связность пространства  в некоторой аффинной системе координат  характеризуются следующими уравнениями:

; ; .                     (14)

Если связности отображаемых пространств без кручений, то ковектор , где - скалярная функция, .

Алгебраические структуры тензоров кривизны (4) - (6), равенства (11) и проективные тензоры кривизны (12) - (14) являются более общими тензорными приказной проективно - точечных или - пространств гиперплоскостных элементов с кручениями.

СПИСОК ЛИТЕРАТУРЫ

1. Ферзалиев А.С. Автоморфизмы пространства гиперплоскостных элементов // Функционально - дифференциональные уравнения и их приложения. Материалы первой Международной научной конференции, Махачкала, ДГУ, 2003.

Библиографическая ссылка