Кобзев В.Н.
355 KB
Пусть (Ω, Σ, Р) - вероятностное пространство, на котором можно определить последовательность Бернулли {en}. Н - гильбертово пространство с базисом {εn}. Определим последовательность случайных элементов соотношением:
ξn = εnen (n ≥ 1) почти наверное (п.н.).
Очевидно ξn → 0 слабо в L2(H). Предположим, что существует подпоследовательность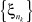 
, подчиняющаяся некоторому (непременно гауссовскому) закону. Обозначим предельное распределение через. Тогда
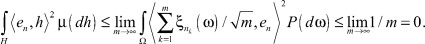
Следовательно, для любого r > 0
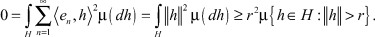
Таким образом, мера μ сосредоточена в нуле. Отсюда вытекает, что
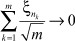
по вероятности. С другой стороны,
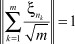п.н.
Налицо противоречие.
Библиографическая ссылка
Кобзев В.Н. ПРИМЕР ОГРАНИЧЕННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ СЛУЧАЙНЫХ ЭЛЕМЕНТОВ, НЕ СОДЕРЖАЩЕЙ ПОДПОСЛЕДОВАТЕЛЬНОСТИ, ПОДЧИНЯЮЩЕЙСЯ НАСЛЕДСТВЕННОМУ ПРЕДЕЛЬНОМУ ЗАКОНУ // Успехи современного естествознания. – 2011. – № 6. – С. 80-80;URL: https://natural-sciences.ru/ru/article/view?id=26947 (дата обращения: 24.04.2024).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
«Международный журнал прикладных и фундаментальных исследований»
ИФ РИНЦ = 0,593
«Международный журнал экспериментального образования»
ИФ РИНЦ = 0,425
«Научное Обозрение. Биологические Науки»
ИФ РИНЦ = 0,400
«Научное Обозрение. Медицинские Науки»
ИФ РИНЦ = 0,801
«Научное Обозрение. Экономические Науки»
ИФ РИНЦ = 0,871
«Научное Обозрение. Педагогические Науки»
ИФ РИНЦ = 0,733
«Научное Обозрение. Технические Науки»
ИФ РИНЦ = 0,695
«European journal of natural history»
ИФ РИНЦ = 0,301