Классические краевые задачи для эллиптических уравнений, такие как задачи Дирихле, Неймана, общая краевая задача перестают быть корректными для уравнений смешанного типа. В работах Н.Н. Вахания [2], J.R. Cannon [10] доказана корректность задачи Дирихле для уравнения Лаврентьева – Бицадзе в прямоугольных областях. А.М. Нахушевым [9] установлено, что задача Дирихле для уравнения Лаврентьева – Бицадзе в конечной смешанной области, ограниченной в верхней полуплоскости 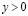 кусочно-гладкой кривой, содержащей интервал (0,1) прямой
кусочно-гладкой кривой, содержащей интервал (0,1) прямой 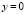 , а гиперболическая часть области квадрат, всегда разрешима и притом единственным образом.
, а гиперболическая часть области квадрат, всегда разрешима и притом единственным образом.
Цель исследования: доказать существование и единственность решения аналога задачи Дирихле для уравнения смешанного параболо – гиперболлического типа.
Постановка задачи. Рассмотрим уравнение
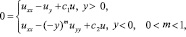 (1)
(1)
где  ,
, 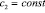 , в конечной области W, ограниченной отрезками А2А1, А1В1, В1В2, В2А2 прямых х=0, у=a>0, x=1, y=–b (b>0), соответственно и характеристиками уравнения (1) при
, в конечной области W, ограниченной отрезками А2А1, А1В1, В1В2, В2А2 прямых х=0, у=a>0, x=1, y=–b (b>0), соответственно и характеристиками уравнения (1) при 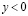
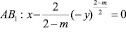 ;
;
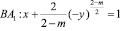 .
.
Обозначим через 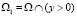 ,
, 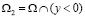 параболическую и гиперболическую части области W соответственно; АВ
параболическую и гиперболическую части области W соответственно; АВ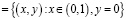 .
.
Задача. В области W найти решение u=u(x,y) из класса
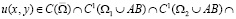
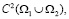
удовлетворяющее краевым условиям
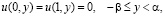 (2)
(2)
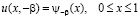 (3)
(3)
и условию сопряжения
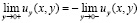 , (4)
, (4)
где 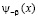 – заданная функция.
– заданная функция.
Теорема 1. Если выполнены условия:
1) 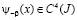 ;
;
2) 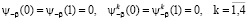 ;
;
3) 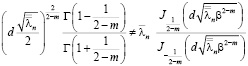 , (5)
, (5)
где 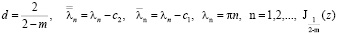 – функции Бесселя первого рода порядка
– функции Бесселя первого рода порядка 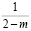 , то решение задачи (1) – (4) существует и единственно.
, то решение задачи (1) – (4) существует и единственно.
Доказательство единственности решения поставленной задачи аналогично [3].
Докажем существование решения задачи (1)-(4).
В области W, решение поставленной задачи будем искать методом разделения переменных.
Решение задачи (1)-(4) выписывается в явном виде
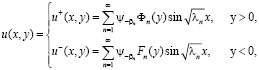 (6)
(6)
где 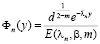 ; (7)
; (7)
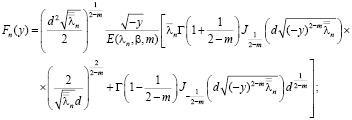 (8)
(8)
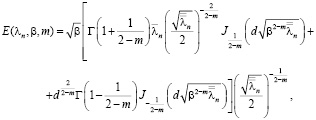
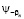 – коэффициенты Фурье функции y-b (х).
– коэффициенты Фурье функции y-b (х).
Ряды (6) также как и ряды, полученные почленным двукратным дифференцированием, сходятся абсолютно и равномерно в Ω1 и Ω2.
В самом деле, покажем, что ряд
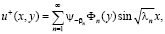 (9)
(9)
где 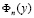 – определяется формулой (7), действительно является регулярным решением задачи (1) – (4) в области Ω1. Для этого ниже мы покажем непрерывность как самой функции
– определяется формулой (7), действительно является регулярным решением задачи (1) – (4) в области Ω1. Для этого ниже мы покажем непрерывность как самой функции 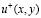 так и ее производных до второго порядка включительно.
так и ее производных до второго порядка включительно.
Используя условия (1), (2) теоремы 1, проинтегрировав равенство
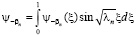
по частям, нетрудно показать, что коэффициенты Фурье 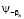 граничной функции y-b (х) не превосходят величины
граничной функции y-b (х) не превосходят величины 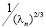 .
.
Пользуясь неравенством
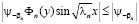 ,
,
заключаем, что ряд
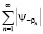 (10)
(10)
является мажорантным для ряда (9). Отсюда заключаем сходимость ряда (10), и, следовательно, равномерномерную сходимость ряда (9), и непрерывность функции 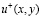 .
.
Аналогично можно установить равномерную сходимость продифференцированных рядов до второго порядка включительно:
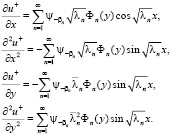
Обратимся теперь к равенству
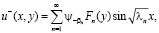 (11)
(11)
где
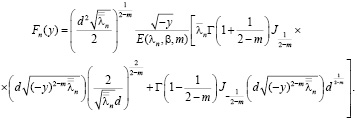
Докажем, что решение, представленное рядом (11), действительно является регулярным в области 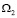 . Для этого мы покажем равномерную сходимость как ряда (11), так и рядов, почленно продифференцированных два раза по переменным х, у, т.е.
. Для этого мы покажем равномерную сходимость как ряда (11), так и рядов, почленно продифференцированных два раза по переменным х, у, т.е.
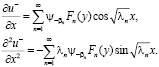
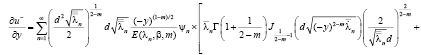
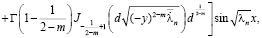
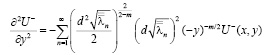 .
.
Известно [1], что функции
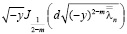
и 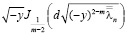
являются непрерывными и ограниченными. Это следует из свойств бесселевых функций первого рода.
Лемма 1. Для всех n и y ∈[-b; 0] существует постоянная k1>0, такая, что
|An(y)| ≤ k1, (12)
где 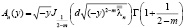 .
.
Доказательство: Из свойств бесселевых функций первого рода, следует, что функция An(y) является непрерывной по переменной у на отрезке [-b; 0] . Следовательно, она ограничена.
При n→ ∝ для любого y∈[-b; 0] функция An(y) является бесконечно малой, порядка 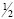 .
.
Действительно,
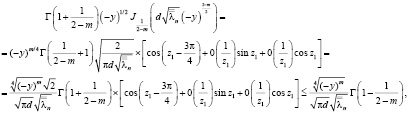
где 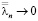 при n→ ∝,
при n→ ∝,
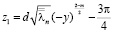 .
.
Таким образом, при всех y∈ [-b; 0] и n∈N постоянная k1 такая, что справедлива оценка (12).Известно, что 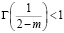 .
.
Справедливы утверждения:
Лемма 2. Для всех n∈N и любого y∈ [-b; 0] существует постоянная k2>0 такая, что
|Вn(y)| ≤ k2 ,
где 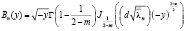 .
.
Лемма 3. Для всех n∈N и любого y∈[-b; 0] существуют постоянные k3>0 и k4>0 такие, что
|Dn(y)| ≤ n k3, |Сn(y)| ≤ n k4,
где
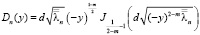 ,
,
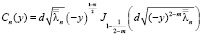
Лемма 4. Для всех n∈N и любого y∈ [-b; 0] существуют постоянные k5>0 и k6>0 такие, что
|Ln(y)| ≤ n2 k5, |Wn(y)| ≤ n2 k6
где
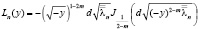 ,
,
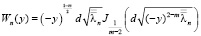
Доказательство лемм 2-4 проводится аналогично доказательству леммы 1.
Предположим, что y-b(х) непрерывно дифференцируема до третьего порядка включительно. В силу того, что y-b(0) =y-b (1)=0 ее можно продолжить непрерывно на интервале [0,1] . Обозначим через 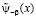 периодическую на всей действительной оси функцию, которая является периодическим продолжением функции y-b(х). Будем предполагать, что
периодическую на всей действительной оси функцию, которая является периодическим продолжением функции y-b(х). Будем предполагать, что 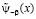 является также непрерывно дифференцируемой функцией до третьего порядка включительно.
является также непрерывно дифференцируемой функцией до третьего порядка включительно.
Продолженную функцию можно представить в виде ряда Фурье на всей оси. При изменении аргумента x в пределах 0≤ х≤ 1 полученный ряд будет совпадать с граничной функцией y-b (х).
Таким образом, с помощью лемм 1–4 и выше приведенной теоремы 1 можно утверждать справедливость следующей теоремы
Теорема 2. Пусть числовой ряд 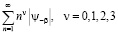 сходится.
сходится.
Тогда:
Ряды u(x,y), ux(x,y), uy(x,y) сходятся абсолютно и равномерно в замкнутой области W.
Ряды uxx(x,y) и uyy(x,y) сходятся абсолютно и равномерно в области W.
Следует отметить, что нелокальные краевые задачи для уравнений смешанного типа исследовались также в работах [4-8].
Библиографическая ссылка
Водахова В.А., Гучаева З.Х. ЗАДАЧА ДИРИХЛЕ ДЛЯ УРАВНЕНИЯ СМЕШАННОГО ПАРАБОЛО-ГИПЕРБОЛИЧЕСКОГО ТИПА С РАЗРЫВНЫМИ КОЭФФИЦИЕНТАМИ // Успехи современного естествознания. 2013. № 11. С. 136-140;URL: https://natural-sciences.ru/ru/article/view?id=33136 (дата обращения: 04.02.2026).



