Рассматривается динамическая обратная задача для уравнения акустики. Для применения градиентного метода Ландвебера, разрабатывается вычислительные методы решения нелинейной обратной задачи акустики. Доказываем условную устойчивость решения системы нелинейных уравнений Вольтерра [1] и определям константы устойчивости (постоянные Липшица).
Определение 1. (Класс решений обратной задачи). Будем говорить, что 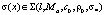 , если s(x) удовлетворяет следующим условиям [5]:
, если s(x) удовлетворяет следующим условиям [5]:
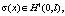
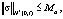
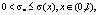
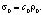
Определение 2. (Класс исходных данных). Будем говорить, что 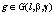 , если g удовлетворяет следующим условиям [5]:
, если g удовлетворяет следующим условиям [5]:
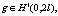
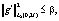
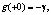
Объекты и методы исследований [6]
Предположим, что для для 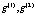 из класса
из класса 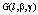 существуют
существуют 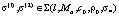 , удовлетворяющие обратной задаче
, удовлетворяющие обратной задаче
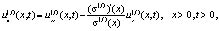 (1)
(1)
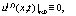 (2)
(2)
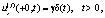 (3)
(3)
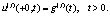 (4)
(4)
для j = 1 и j = 2.
Учитывая, что
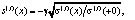 ,
,
обозначим
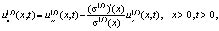
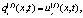
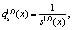
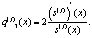 (5)
(5)
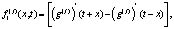
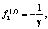
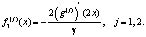
Поскольку 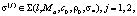 то в силу обозначений можно оценить
то в силу обозначений можно оценить
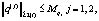 (6)
(6)
где 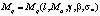 . Пусть вектор-функция
. Пусть вектор-функция 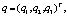 удовлетворяет системе
удовлетворяет системе
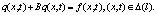 (7)
(7)
Решение задачи Aq = f предполагается, но утверждается, что существует единственное устойчивое решение для данных из окрестности точно заданных, то есть накладывается ограничение на шум во входных данных.
Для условной корректности рассматриваемой задачи, в отличие от аналогичной теоремы в [2] в нижеприведенной теореме при выводе требуемой константы в основном неравенстве использовалась не оценка вектора q, а оценки
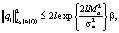
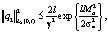
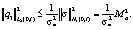
каждой из его компонент q1, q2, q3. В работе [2] в выкладках норма каждой компоненты оценивалась через норму вектора q, так как оценка нормы вектора q есть сумма оценок его компонент. А в данной статье, как сказано, выше, уже использовались непосредственно оценки каждой из его компонент q1, q2, q3
Теорема. Предположим, что для 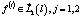 , существуют решения обратной задачи
, существуют решения обратной задачи 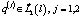
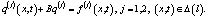 (8)
(8)
Тогда
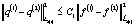 (9)
(9)
Здесь
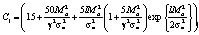
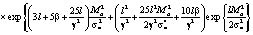
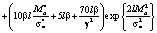
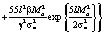 . (10)
. (10)
Доказательство. Введем
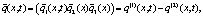
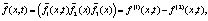
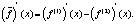
Тогда из (8) следует
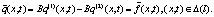
Оценим первую компоненту 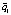 :
:
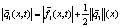
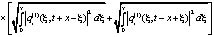 +
+
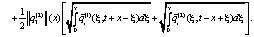
Учитывая, что 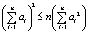 для
для 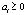 , получим
, получим
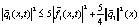
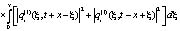 +
+
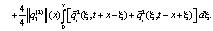 (11)
(11)
Имеем
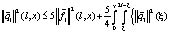
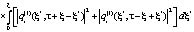 ×
×
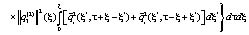 ≤
≤
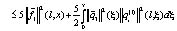
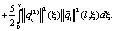 (12)
(12)
Оценим вторую компоненту:
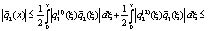
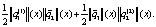
Следовательно,
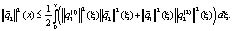 (13)
(13)
Оценим 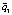 :
:
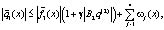 (14)
(14)
где
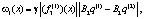
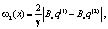
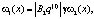
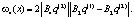
Во-первых, мы имеем
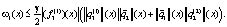
Во-вторых,
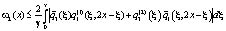
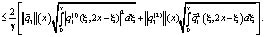 (15)
(15)
В-третьих,
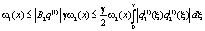
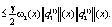 (16)
(16)
В-четвертых,
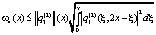
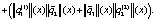 (17)
(17)
Принимая во внимание 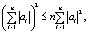
получим 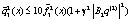
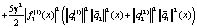
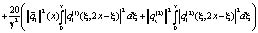
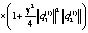
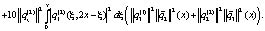
Таким образом, имеем
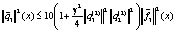
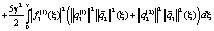
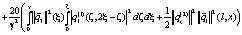
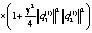
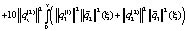
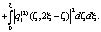
Для удобства обозначим
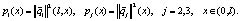
Введем обозначения
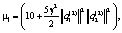
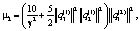
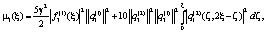
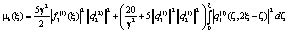
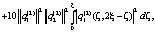 (18)
(18)
Введем функцию
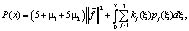 (19)
(19)
Следовательно [3]
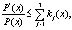
и, применяя неравенство Гронуолла, получим
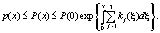
С другой стороны, учитывая равенство
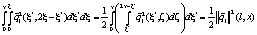
имеем
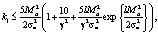
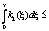
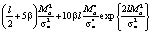
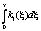
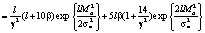
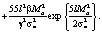
Таким образом, получаем
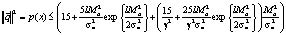 ×
×
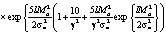
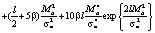 +
+
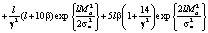
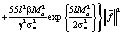 =
=
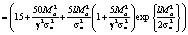
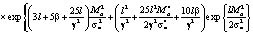
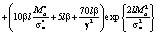
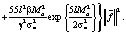
Получим оценку для 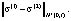
По лемме Гронуолла имеем
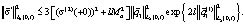
В итоге получаем
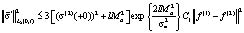
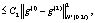 (20)
(20)
где
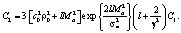
Учитывая, что 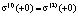 получим
получим
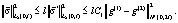 (21)
(21)
Складывая оценки получим
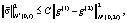
где 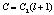 .
.
Результаты и их обсуждение
Теорема 1.5. Пусть для 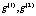 из класса
из класса 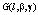 существуют
существуют
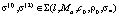
как решения обратной задачи (1)–(4) соответственно. Тогда
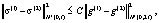
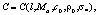
где
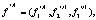
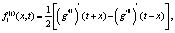
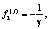
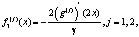
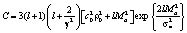 ×
×
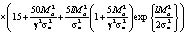 ×
×
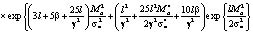
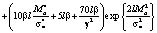 +
+
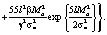
Заключение, выводы. Для доказательства условной корректности рассматриваемой задачи, доказано теорема, где в отличие от аналогичной теоремы в [3] в вышеприведенной теореме при выводе требуемой константы в основном неравенстве использовалась не оценка вектора q, а оценки каждой из его компонент 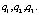 В работе [3] в выкладках норма каждой компоненты оценивалась через норму вектора q, так как оценка нормы вектора q есть сумма оценок его компонент. А в данной работе, как сказано, выше, уже использовались непосредственно оценки каждой компоненты.
В работе [3] в выкладках норма каждой компоненты оценивалась через норму вектора q, так как оценка нормы вектора q есть сумма оценок его компонент. А в данной работе, как сказано, выше, уже использовались непосредственно оценки каждой компоненты.
Библиографическая ссылка
Тюлепбердинова Г.А., Абишева А.Ж. УСЛОВНАЯ КОРРЕКТНОСТЬ ОБРАТНОЙ ЗАДАЧИ АКУСТИКИ // Успехи современного естествознания. 2014. № 3. С. 175-180;URL: https://natural-sciences.ru/ru/article/view?id=33284 (дата обращения: 04.03.2026).



