2826 KB
В пространстве 
комплексных переменных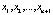 
рассмотрим дифференциальное уравнение порядка 2p вида
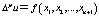, (1)
где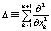 
– оператор Лапласа, 
, 
, 
.
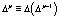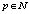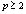Точку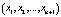 
пространства 
обозначим для краткости (X, z), где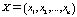 
, 
.
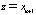Предположим, что функция f(X,z) голоморфна в некоторой открытой в пространстве 
окрестности H(D) кругового полицилиндра
.
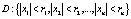Для уравнения (1) рассмотрим задачу Коши в следующей постановке: найти голоморфное решение u уравнения (1), удовлетворяющее начальным условиям
, 
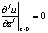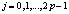. (2)
Теорема. Если функция f(X,z) голоморфна в области H(D), то для решения задачи Коши (1), (2) справедливо представление
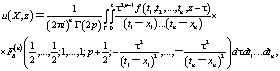
где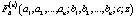 
– гипергеометрическая функция Лауричелла, а интегрирование совершается по остову Г границы полицилиндра D.
Библиографическая ссылка
Шалагинов С.Д. ЗАДАЧА КОШИ ДЛЯ НЕОДНОРОДНОГО ПОЛИГАРМОНИЧЕСКОГО УРАВНЕНИЯ В КОМПЛЕКСНОМ ПРОСТРАНСТВЕ // Успехи современного естествознания. – 2014. – № 3. – С. 208-208;URL: https://natural-sciences.ru/ru/article/view?id=33310 (дата обращения: 18.04.2024).
Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»
(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)
«Международный журнал прикладных и фундаментальных исследований»
ИФ РИНЦ = 0,593
«Международный журнал экспериментального образования»
ИФ РИНЦ = 0,425
«Научное Обозрение. Биологические Науки»
ИФ РИНЦ = 0,400
«Научное Обозрение. Медицинские Науки»
ИФ РИНЦ = 0,801
«Научное Обозрение. Экономические Науки»
ИФ РИНЦ = 0,871
«Научное Обозрение. Педагогические Науки»
ИФ РИНЦ = 0,733
«Научное Обозрение. Технические Науки»
ИФ РИНЦ = 0,695
«European journal of natural history»
ИФ РИНЦ = 0,301