Будем считать, что структурные состояния в случае детерминистических модулярных структур в каждой ячейке-параллелепипеде структурированного 3D пространства определяются возможными кристаллическими r, наноразмерными n и фрактальными f компонентами с помощью задания соответствующих генераторов [1–6]. Возможные структурные состояния в 1D пространстве могут быть комбинаторно перечислены и представлены следующей схемой.
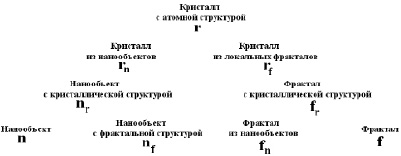
Квадратная матрица возможных состояний А = ||aij|| содержит 9 разных состояний
 ,
,
а соответствующая ей матрица Z = ||zij|| законов распределения объектов выглядит следующим образом:

Условный размерный параметр D может быть рассчитан для каждого структурного состояния следующим образом:
– для кристаллической компоненты r
D(r) = 1;
– для фрактальной компоненты f и состояний rf и сопряженного с ним rf* = fr он полностью совпадает с фрактальной размерностью:
D(rf) = D(fr) = D(r) D(f) = DimRf = = Dim (GenRf) < 1;
– для наноразмерной компоненты n и состояний rn и и сопряженного с ним rn* = nr имеем
D(nr) = D(rn) = D(r) D(n) = (<n>/no) < 1,
если средний размер нанообъекта <n> < no = 100 нм и
D(r) D(n) = 1,
если <n> ³ no;
– для двух сопряженных состояний fn (фрактал из нанообъектов) и nf = fn* (нанообъект из локальных фракталов) размерный параметр определяется следующим образом:
D(fn) = D(nf) = D(f) D(n) = =(<n>/no) Dim (GenRf) < 1.
С учетом всех вариантов структурно совместимых сочетаний из двух компонент перечислим основные классы вероятных структурных состояний в 2D пространстве [1, 2]:
• кристаллический (r r),
• кристаллический наноразмерный (r n),
• кристаллический фрактальный (r f),
• фрактальный гибридный (f f),
• фрактальный наноразмерный (f n) и
• наноразмерный (n n).
Квадратная матрица возможных состояний А = ||aij||aij|||| в 2D пространстве содержит всего N = 32d = 81 ориентационно различимых состояний,
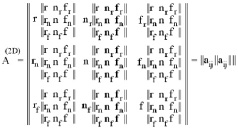
из которых 45 – состояния разного вида, принадлежащие шести указанным выше классам. Перечислим возможные структуры и их симметрию [7], охарактеризуем представителей этих видов состояний, соподчиненные (∈) и сопряженные им (*) состояния.
1 Класс кристаллический (r r), структуры Rrr2 (симметрия плоских групп G22):
(r r) – 2D-кристалл из атомных цепочек, (r r)* = (r r), (r r) ∈ (nr nr),
(r rn) – 2D-кристалл из 1D-нанофрагментов, (r rn)* = (r nr), (r rn) ∈ (nr n),
(r rf) – 2D-кристалл из 1D локальных фракталов, (r rf)* = (r fr), (r rf) ∈ (nr nf),
(rn rn) – 2D-кристалл из наноразмерных частиц, (rn rn)* = (nr nr), (rn rn) ∈ (n n),
(rn rf) – 2D-кристалл из 1D-нанофрагментов и 1D локальных фракталов, (rn rf)* = (nr fr), (rn rf) ∈ (n nf),
(rf rf) – 2D-кристалл из локальных фракталов (детерминистическая фрактальная структура), (rf rf)* = (fr fr), (rf rf) ∈ (nr nr).
2 Класс кристаллический наноразмерный (r n), структуры Rrn2 (симметрия плоских групп G22 или групп бордюров G21):
(r n) – 2D структура из упорядоченных цепочек нанообъектов, (r n)* = (r n), (r n) ∈ (nr n),
(r nr) – 2D структура из упорядоченных цепочек кристаллических нанообъектов, (r nr)* = (r rn), (r nr) Î (nr nr),
(r nf) – 2D структура из упорядоченных цепочек фрактальных нанообъектов, (r nf)* = (r fn), (r nf) ∈ (nr nf),
(rn n) – 2D структура из 1D-фрагментов нанообъектов, (rn n)* = (nr n), (rn n) ∈ (n n),
(rn nr) – 2D структура из 1D-фрагментов кристаллических нанообъектов, (rn nr)* = (nr rn), (rn nr) ∈ (n nr),
(rn nf) – 2D структура из 1D-фрагментов фрактальных нанообъектов, (rn nf)* = (nr fn), (rn nf) ∈ (n nf),
(rf n) – 2D структура из нанообъектов, упорядоченных по фрактальному закону (rf n)* = (fr n), (rf n) ∈ (nf n),
(rf nr) – 2D структура из кристаллических нанообъектов, упорядоченных по фрактальному закону, (rf nr)* = (fr rn), (rf nr) ∈ (nf nr),
(rf nf) – 2D структура из фрактальных нанообъектов, упорядоченных по фрактальному закону, (rf nf)* = (fr fn), (rf nf) ∈ (nf nf).
3 Класс кристаллический фрактальный (r f), структуры Rrf2 (симметрия плоских групп G22, групп бордюров G21 или точечных групп бордюров G21,0):
(r f) – 2D структура из упорядоченных 1D фракталов, (r f)* = (r f),
(r fr) – 2D структура из упорядоченных 1D детерминистических фракталов, (r fr)* = (r rf),
(r fn) – 2D структура из упорядоченных 1D фрактальных нанообъектов, (r fn)* = (r nf),
(rn f) – 2D структура из 1D фракталов, упорядоченных в 1D нанофрагменте, (rn f)* = (nr f),
(rn fr) – 2D структура из 1D детерминистических фракталов, упорядоченных в 1D нанофрагменте, (rn fr)* = (nr rf),
(rn fn) – 2D структура из 1D фрактальных нанообъектов, упорядоченных в 1D нанофрагменте, (rn fn)* = (nr nf),
(rf f) – 2D структура из 1D фракталов, упорядоченных по фрактальному закону, (rf f)* = (fr f),
(rf fr) – 2D структура из 1D детерминистических фракталов, упорядоченных по фрактальному закону, (rf fr)* = (rf fr),
(rf fn) – 2D структура из 1D фрактальных нанообъектов, упорядоченных по фрактальному закону, (rf fn)* = (fr nf).
4 Класс фрактальный гибридный (f f), структуры Rff2 (симметрия плоских групп G22, групп бордюров G21 или точечных групп бордюров G21,0):
(f f) – 2D фрактальная гибридная структура, (f f)* = (f f),
(f fr) – 2D фрактал из 1D детерминистических фракталов, (f fr)* = (f rf),
(f fn) – 2D фрактал из 1D фрактальных нанообъектов, (f fn)* = (f nf),
(fr fr) – 2D детерминистический фрактал, (fr fr)* = (rf rf),
(fr fn) – 2D фрактал из 1D детерминистических фракталов и из 1D фрактальных нанообъектов, (fr fn)* = (rf nf),
(fn fn) – 2D фрактал из 2D фрактальных нанообъектов, (fn fn)* = (nf nf).
5 Класс фрактальный наноразмерный (f n), структуры Rfn2 (симметрия групп бордюров G21 или точечных групп бордюров G21,0):
(f n) – 2D фрактальная структура из нанообъектов, (f n)* = (f n),
(f nr) – 2D фрактал из 1D-фрагментов структуры, (f nr)* = (f rn),
(f nf) – 2D фрактал из 1D локальных фракталов, (f nf)* = (f fn),
(fn n) – 2D фрактальный нанообъект из 1D нанообъектов, (fn n)* = (nf n),
(fn nr) – 2D фрактальный нанообъект из 1D-фрагментов структуры (fn nr)* = (nf rn),
(fn nf) – 2D фрактальный нанообъект из 1D локальных фракталов, (fn nf)* = (fn nf),
(fr n) – 2D структура из 1D детерминистических фракталов и нанообъектов, (fr n)* = (rf n),
(fr nr) – 2D структура из 1D детерминистических фракталов1D-фрагментов структуры, (fr nr)* = (rf rn),
(fr nf) – 2D структура из 1D детерминистических фракталов и 1D локальных фракталов, (fr nf)* = (rf fn).
6 Класс наноразмерный (n n), структуры Rnn2 (симметрия точечных 2D или розеточных групп G20):
(n n) – 2D-наночастица, (n n)* = (n n),
(n nr) – 2D-нанообъект из 1D-фрагмента структуры, (n nr)* = (n rn),
(n nf) – 2D-нанообъект из 1D локального фрактала, (n nf)* = (n fn),
(nr nr) – 2D-нанофрагмент структуры, (nr nr)* = (rn rn),
(nr nf) – 2D-нанообъект из 1D-фрагмента структуры и 1D локального фрактала, (nr nf)* = (rn fn),
(nf nf) – 2D локальный фрактал, (nf nf)* = (fn fn).
Условный размерный параметр
D = dr D(r) + df D(f) + dn D(n),
где dr, df и dn [0, 2] – количества соответствующих компонент одного сорта,
В случае состояний со структурно совместимыми разными фрактальными компонентами класса (f1 f2) могут сформироваться транзитивные фрактальные структуры Tr[R(f1,f2)] [1 – 4] и соответствующие размерные параметры тогда определяются следующим образом:
D = D(f1) + D(f2) = =Dim(Tr[Gen(f1),Gen(f2)]).
Ранее в [8–15] представления о состояниях поверхности композитов, обусловленных как кристаллическими фазами (состояния класса (r r)), так и распределенными определенным образом наночастицами некоторых из этих фаз (состояния класса (r n)), а также квазифракталами-конфигурациями межфазных границ (состояния класса (r f)), были использованы при целенаправленном поиске и интерпретации трибологических свойств поверхности композиционных материалов и покрытий на основе систем Ni-P и Ni-B.
Библиографическая ссылка
Иванов В.В. ВОЗМОЖНЫЕ ПРОСТРАНСТВЕННЫЕ КОМПОНЕНТЫ СТРУКТУРНЫХ СОСТОЯНИЙ ПОВЕРХНОСТИ КОМПОЗИЦИОННЫХ МАТЕРИАЛОВ И ПОКРЫТИЙ // Успехи современного естествознания. 2014. № 7. С. 126-128;URL: https://natural-sciences.ru/ru/article/view?id=34159 (дата обращения: 15.02.2026).



