Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Валеев А.А. 1

---

1 ФГОБУ ВПО «Волгоградский государственный технический университет»

Данная работа посвящена расчету КАРС-откликов Qполос 1285 см1 и 1388 см1 фермиевского дублета ν1/2ν2 двуокиси углерода, сформированных под действием упругой дефазировки вблизи критической точки. Показано, что критическое уширение не чувствительно к малым отклонениям по температуре и плотности от критической точки.

Статья в формате PDF

2937 KB

критические явления

двуокись углерода

КАРС

1. Arakcheev V.G., Bagratashvili V.N., Valeev A.A., Gordiyenko V.M., Kireev V.V., Morozov V.B., Olenin A.N., Popov V.K., Tunkin V.G., Yakovlev D.V. // J. Raman Spectrosc. 2003. Т. 34. № 12. С. 952.

2. Аракчеев В.Г., Баграташвили В.Н., Валеев А.А., Гордиенко В.М., Киреев В.В., Морозов В.Б., Оленин А.Н., Попов В.К., Тункин В.Г., Яковлев Д.В. // Quantum Electronics. 2004. Т. 34. № 1. С. 86.

3. Arakcheev V.G., Kireev V.V., Morozov V.B., Olenin A.N., Tunkin V.G., Valeev A.A., Yakovlev D.V. // J. Raman Spectrosc. 2007. Т. 38. № 8. C. 1046.

4. Валеев А. // Научно-технический вестник Поволжья. 2013. № 3. C. 18.

5. Morozov V., Mochalov S., Olenin A., Tunkin V., Kouzov A. // J. Raman Spectrosc. 2003. Т. 34. № 12. C. 983.

6. Chang R.F., Burstyn H., Sengers J.V. // Phys. Rev. A. 1979. Т. 19. № 2. C. 866.

7. Clouter M.J., Kiefte H., Ali N. // Phys. Rev. Lett. 1978. Т. 40. № 18. С. 1170.

8. Clouter M.J., Kiefte H. // Phys. Rev. Lett. 1984. Т. 52. № 9. С. 763.

9. Clouter M.J., Kiefte H., Deacon. C.G. // Phys. Rev. A. 1986. Т. 33. № 4. С. 2749.

10. Fenghour A., Wakeham W.A., Vesovic V. // J. Phys. Chem. Ref. Data. 1998. Т. 27. № 8. C. 31.

11. Fisher M.E., Burford R.J. // Phys. Rev. 1967. Т. 156. № 2. C. 583.

12. Fisher M.E., Zinn S. // J. Phys. A. 1998. Т. 31. № 37. C. L629.

13. Garrabos Y., Palencia F., Lecoutre C., Erkey C., Le Neindre B. // Phys. Rev. E. 2006. Т. 73. № 2. C. 026125.

14. Luettmer-Strathmann J., Sengers J.V., Olchowy G.A. // J. Chem. Phys. 1995. Т. 103. № 17. C. 7482.

15. Lunacek J.H., Cannell D.S. // Phys. Rev. Lett. 1971. Т. 27. № 13. C. 841.

16. Maccabee B.S., White J.A. // Phys. Rev. Lett. 1971. Т. 27. № 8. C. 495.

17. Moldover M.R., Sengers J.V., Gammon R.W., Hocken R.J. // Rev. Mod. Phys. 1979. Т. 51. № 1. С. 79.

18. Mukamel S., Stern P.S., Ronis D. // Phys. Rev. Lett. 1983. Т. 50. № 8. C. 590.

19. Musso M., Asenbaum A., Keutel D., Seifert F., Oehme K.-L. // Phys. Rev. Lett. 1996. Т. 77. № 1. C. 2746.

20. Musso M., Matthai F., Keutel D., Oehme K.-L. // J. Chem. Phys. 2002. Т. 116. № 18. С. 8015.

21. Nakayama H., Saitow K., Sakashita M., Ishii K., Nishikawa K. // Chem. Phys. Lett. 2000. Т. 320. № 3-4. С. 323.

22. Nishikawa K., Morita T. // Chem. Phys. Lett. 2000. Т. 316. №№ 3-4. C. 238.

23. Olchowy G.A., Sengers J.V. // Phys. Rev. Lett. 1988. Т. 61. № 1. С. 15.

24. Saitow K., Nakayama H., Ishii K., Nishikawa K. // J. Phys. Chem. A. 2004. Т. 108. № 27. С. 5770.

25. Span R., Wagner W. // J. Phys. Chem. Ref. Data. 1996. Т. 25. № 6. C. 1509.

26. Staniaszek P., Clouter M.J., Kiefte H. // Can. J. Phys. 1988. Т. 66. № 4. C. 358.

27. Strauss H.L., Mukamel S. // J. Chem. Phys. 1984. Т. 80. № 12. C. 6328.

28. Vesovic V., Wakeham W.A., Olchowy G.A., Sengers J.V., Watson J.T.R., Millat J. // J. Phys. Chem. Ref. Data 1990. Т. 19. № 3. C. 763.

29. Wood K.A., Strauss L. // J. Chem. Phys. 1983. Т. 78. № 6. С. 3455.

30. Yu Yang-Xin, Gao Guang-Hua. // Fluid Phase Equilibria. 1999. Т. 166. № 1. C. 111.

Рассеяние света уверенно зарекомендовало себя как инструмент для исследования флуктуаций плотности и их динамики вблизи критической точки фазового перехода газ-жидкость. В последнее время несколько научных коллективов осуществили измерения ширины комбинационно активных переходов разных сред в ее окрестности [1,2,21,19,29,24,7,8,9,20,26]. В отличие от O₂ [7], N2 [8,9,20], и HD [26]; двуокись углерода [1,2,21] (Q-полоса 1388 см^-1) наряду с N₂O [19], этаном [29] и CHF₃ [24] не проявляет явным образом критического уширения. Этому факту до сих пор не удалось получить объяснения. В настоящей и последующих за ней работах будет показано, как можно оценить критическое уширение и учесть его роль в формировании КАРСспектра Q-полосы фермиевского дублета ν₁/2ν₂ двуокиси углерода.

Критическое уширение рассматриваемой Q-полосы уже было качественно рассмотрено в работах Х. Л. Штрауса и Ш. Мукамела [27].

Полный спектральный отклик формируется под влиянием следующих факторов: эффекта Доплера, вращательно-колебательного взаимодействия, ориентационно-колебательного взаимодействия, неупругой передачи энергии, упругой дефазировки. Было обнаружено [5] и определено [3], что вращательно-колебательное взаимодействие Q-полосы 1285 см^-1 существенно отличается от такового Q-полосы 1388 см^-1, что явилось неожиданным результатом. Тем не менее, при плотностях более 0.2ρ_c (ρ_c – критическая плотность), двумя первыми факторами, формирующими спектральный отклик, можно пренебречь в связи с коллапсом. [5] Ориентационно-колебательное взаимодействие растет с плотностью и является заметным, в данном случае, при плотностях выше критической. Упругая дефазировка при плотностях, близких к ρ_c, обусловлена преимущественно флуктуациями плотности. Особенности этого канала дефазировки вблизи критической точки представлены в работах [18] и [4]. В рамках данной работы рассмотрение ограничится только им. Диапазоном исследования настоящей работы является область, прилегающая к критической точке. Рассмотрение ограничено температурами выше критической.

Дефазировка

Для расчета упругой дефазировки флюид представляется в виде N двухуровневых частиц, взаимодействующих парными аддитивными силами со сферически симметричными потенциалами. Основное состояние обозначим как 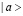, возбужденное – как 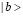. Мы обозначим взаимодействие двух атомов в состоянии 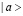с помощью 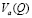, а одного атома в состоянии 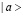и другого – в состоянии 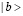с помощью 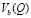; тогда взаимодействие, ответственное за уширение спектра, можно записать в виде .

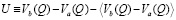Здесь Q – расстояние между атомами. В этом выражении сделано предположение, что состояние частицы не влияет на ее траекторию. Форма спектрального отклика данной системы может быть представлена в следующем виде [4]:

,

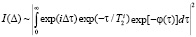где 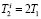– время дефазировки, обусловленной неупругой передачей энергии.

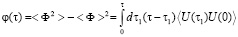, (1)

где 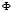– случайный фазовый сдвиг дефазируемого перехода.

В пределе однородного уширения, член 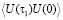в 1 уменьшается в e раз за время 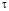, при котором 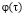значительно меньше 1. Для много больших значений 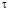можно записать

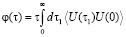. (2)

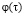будет рассчитан с помощью уравнения (11) в [4]. Для верхнего предела k использована следующая оценка

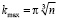, (3)

где n – средняя численная плотность.

Уравнения состояния [25, 10, 28] позволяют рассчитать не только сжимаемость, но и термическую диффузию. Уравнение состояния [30], использованное для определения самодиффузии, дает точность 7 %. 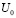(ур-е (10) в [4]) было оценено из спектроскопических наблюдений,

,

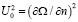где Ω – средняя частота спектрального профиля.

Значение 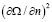несколько изменяется при переходе плотности через околокритическую область. К сожалению, на данный момент, не получено точных данных для околокритических температур. Таким образом, значения 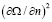в данной работе полагаются независимыми от плотности для каждой Q-полосы.

Уравнение (11) в [4] содержит длину корреляции. Значения и формулы расчета корреляционной длины для CO₂ были опубликованы в нескольких статьях. Одни работы [16, 15, 13] ограничены рассмотрением исключительно случая критической изохоры, в то время как область исследования других [23, 14, 12, 22] распространяется вне изохоры. Уравнение (6.10) из [14] позволяет рассчитать длину корреляции,

,

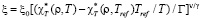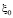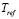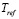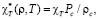
где =1.5Å, Г=0.0481, – опорная температура, подобранная таким образом, что критическое увеличение теплопроводности пренебрежимо мало для температур, больших , 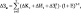симметризованная изотермическая сжимаемость, γ=1.239 и ν=0.630 – критические индексы. В настоящей работе использовано 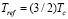. Примеры расчета корреляционной длины показаны на рис. 1. Полученные результаты количественно согласуются с экспериментальными данными [22] (рис. 1, кружки) в диапазоне, где аппроксимирующая функция статического структурного фактора Фишера-Бурфорда (уравнение (8) в [18], см. также [11,6]) чувствительна к длине корреляции (т. е. где последняя больше среднего межатомного расстояния ≈5 Å).

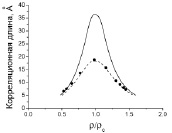
Рис. 1. Длина корреляции в CO₂ как функция приведенной плотности для температур 33 °C (рассчитанные результаты показаны сплошной линией) и 37.1 °C (1.02 Tc) (рассчитанные и экспериментальные результаты показаны штриховой линией и кружками, соответственно)

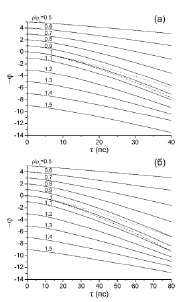
Рис. 2. Рассчитанные логарифмические отклики φ Q-полос 1285 см^-1 (а) и 1388 см^-1 (б) фермиевского дублета ν₁/2ν₂ CO₂ для температуры 33 ^○C. Графики надписаны значениями приведенной плотности и сдвинуты по вертикали для удобства. Штриховыми и пунктирными линиями показаны отклики для температур 32 °C и 36 °C, соответственно

Рассчитанные логарифмические отклики φ Q-полос 1285 см^-1 и 1388 см^-1 фермиевского дублета ν₁/2ν₂ для температуры 33 °C показаны на рис. 2. Как ожидалось [18], отклики сильнее проявляют неоднородные свойства вблизи критической точки. Отклики при температуре 32 °C не демонстрируют значимых различий на временах, при которых уровень отклика больше, чем 1/e от начального. Данный факт свидетельствует о том, что критическое уширение не чувствительно к малым отстройкам температур относительно критической. То же самое справедливо, когда смещение относительно критической точки берется по плотности. Таким образом, температуру 33 °C можно считать «эквивалентной критической» с точки зрения спектроскопии. Существует еще две причины выбора данной температуры. Первая состоит в более высокой точности определения плотности во время эксперимента (исходя из известных давления и температуры) чем для температур, более близких к критической. Вторая заключается в том, что для данной температуры (согласно всем известным экспериментальным данным) отсутствует значительный градиент плотности по высоте [17] и в полной мере справедлива современная теория околокритического поведения двуокиси углерода [15].

Заключение

В настоящей работе рассчитаны КАРС-отклики Q-полос 1285 см^-1 и 1388 см-1 фермиевского дублета ν₁/2ν₂ двуокиси углерода, сформированные под действием упругой дефазировки вблизи критической точки. Новые данные термодинамических свойств и корреляционной длины, доступные на сегодняшний день, позволяют расширить область исследования по плотности и температуре вдаль от критической точки. Показано, что критическое уширение не чувствительно к температуре и плотности вблизи критической точки.

Библиографическая ссылка