Научный журнал

Успехи современного естествознания

ISSN 1681-7494

"Перечень" ВАК

ИФ РИНЦ = 0,775

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Водахова В.А. 1 Нахушева Ф.М. 1 Гучаева З.Х. 1

---

1 ФГБОУ ВПО «Кабардино-Балкарский государственный университет им. Х.М. Бербекова»

Для вырождающегося гиперболического уравнения исследован вопрос о существовании решения задачи с нелокальными условиями на характеристиках для уравнения Бицадзе-Лыкова.

Статья в формате PDF

2551 KB

краевая задача

оператор дробного интегрирования

оператор дробного дифференцирования

задача Коши

уравнение Фредгольма

уравнение Бицадзе-Лыкова

1. Бицадзе А.В. некоторые классы уравнения в частных производных. – М.: Наука, 1981.

2. Водахова В.А., Гучаева З.Х. Задача Дирихле для уравнения смешанного параболо–гиперболического типа с разрывными коэффициентами // Успехи современного естествознания. – 2013. – №11. – С. 136–140.

3. Водахова В.А., Шамеева К.А. Задачи со смещением для системы уравнений первого порядка Лыкова // Известия Кабардино–Балкарского научного центра РАН. – 2013. – №2(52). – С.3–7.

4. Водахова В.А., Гучаева З.Х. Нелокальная задача со смещением для нагруженного уравнения третьего порядка с кратными характеристиками // Успехи современного естествознания. – 2014. – №7. – С. 90–92.

5. Гучаева З.Х., Бесланеева Л.Ю. Нелокальная задача для вырождающегося гиперболического уравнения с операторами дробного интегро–дифференцирования в краевом условии// Успехи современного естествознания. – 2014. – №3. – С.81–87.

6. Мусхелишвили Н.И. Сингулярные интегральные уравнения.– М.: Физматиз, – 1962.

7. Нахушев A.M. Задачи со смещением для уравнений в частных производных.– М.: Наука, –2006. –287с.

8. Репин О.А., Кумыкова С.К. О задаче с обобщенными операторами дробного дифференцирования для вырождающегося внутри области гиперболического уравнения // Вестник Самарского государственного университета. Естественнонаучная серия. – 2012. – №9 (100). – С.52–60.

9. Репин О.А., Кумыкова С.К. Задача с обобщенными операторами дробного дифференцирования для уравнения Бицадзе–Лыкова // Доклады Адыгской (Черкесской) Международной академии наук. – 2014. – Т. 16. – №91. – С.24–32.

10. Репин О.А., Кумыкова С.К. Нелокальная задача с дробными производными дробного для уравнения смешанного типа // Известия высших учебных заведений. Математика. – 2014. – №8. – С.79–85.

11. Репин О.А., Кумыкова С.К. Задача со смещением для вырождающегося внутри области гиперболического уравнения // Вестник Самарского государственного технического университета. Серия «Физико–математические науки». – 2014. – №1 (34). – С.37–47.

12. Самко С. Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения – Минск: Наука и техника, 1987. – 688 с.

Постановка задачи

Рассмотрим уравнение

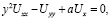(1)

где 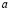– действительная постоянная, причем 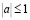, в характеристическом двуугольнике, ограниченном характеристиками AC, BC уравнение (1), выходящими из точки C(1/2, 1), и характеристиками AD, BD, выходящими из точки D (1/2, –1).

Пусть

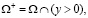
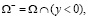
I – интервал 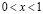прямой .

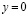Задача. Найти решение

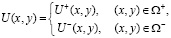
уравнения (1) из класса

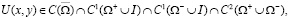
удовлетворяющее краевым условиям:

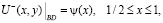(2)

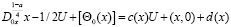(3)

и условию сопряжения

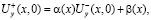(4)

где 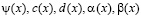– заданные функции, причем

∈

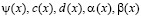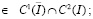
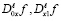– операторы дробного в смысле Римана – Лиувилля интегро-дифференцирования [12], 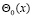– аффикс точки пересечения характеристики уравнения (1), выходящей из точки 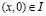, с характеристикой АС.

Отметим, что задача относится к классу краевых задач со смещением сформулированных А.М. Нахушевым [7].

Нелокальные задачи для вырождающихся гиперболических уравнений рассматривались и другими авторами [2–5, 8–11].

Доказательство единственности решения задачи

Теорема. В области 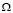не может существовать более одного решения задачи, если

,

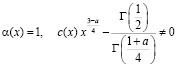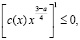
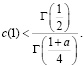
Доказательство. Для доказательства единственности решения задачи воспользуемся методикой, приведенной в работах [8–11].

Пусть

, , .

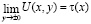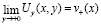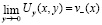Пусть 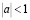. Известно, что решение задачи Коши для уравнения (1) имеет вид [1].

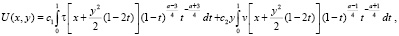(5)

где

.

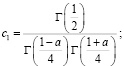
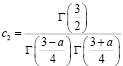Удовлетворяя (5) краевому условию (2), будем иметь

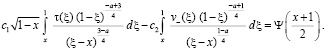(6)

Вычислим

.

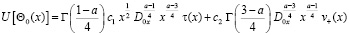Подставляя 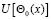в краевое условие (3), будем иметь

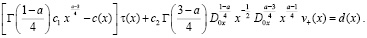(7)

Преобразовав (7) с учетом свойств операторов дробного интегро-дифференцирования, получим

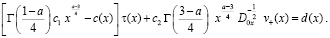(8)

Преобразовав (6), из области 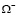получим соотношение, принесенное на J

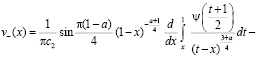
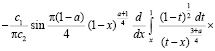(9)

.

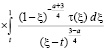После дальнейших упрощений (9) примет вид:

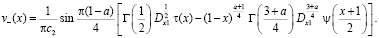(10)

Подействовав на обе части (8) оператором 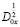будем иметь:

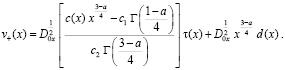(11)

Таким образом, функциональные соотношения между 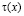и 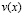, принесенные на част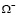и и 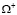смешанной области 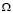имеют вид (10), (11) или при 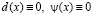соответственно

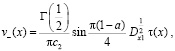(12)

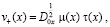(13)

где

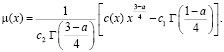
Докажем теорему единственности. Рассмотрим интеграл

.

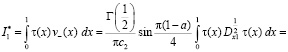
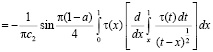С учетом обозначения

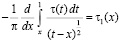
и воспользовавшись известной формулой для функции :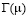

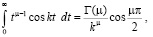
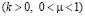. (14)

Полагая в ней 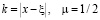, вычислениями, аналогичным [10-11] , получим:

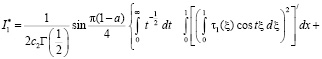
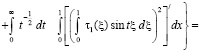
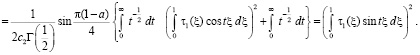
Отсюда заключаем, что .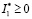

Точно также, обозначив

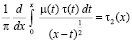
будем иметь

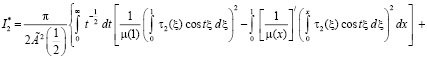
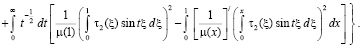
Отсюда видно, что при выполнении условий теоремы 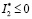. А так как при

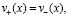то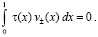

Поскольку слагаемые в 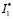неотрицательны, то они также равны нулю. В частности,

.

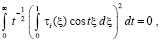
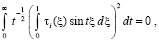
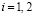Так как 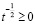, то

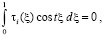
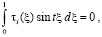
для всех 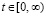, в частности, при 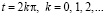. При таких значениях 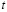функции 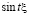, 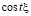образуют полную ортогональную систему функций в .

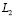Следовательно, 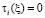почти всюду, а так как они непрерывны по условию, то 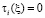всюду. Отсюда нетрудно усмотреть, что 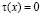и, следовательно, и .

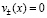Таким образом, 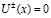как решения задачи Коши с нулевыми данными и, следовательно, решение задачи (1) – (4) единственно.

Доказательство существования решения задачи

Удовлетворив (10), (11) условию сопряжения (4), а затем подействовав на обе части уравнения оператором 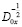, получим

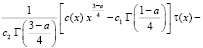
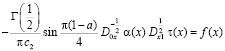, (15)

где

.

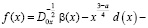
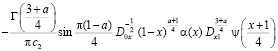Уравнение (15) с учетом свойств операторов дробного интегро-дифференцирования и исследования правой части эквивалентно редуцируется к сингулярному интегральному уравнению

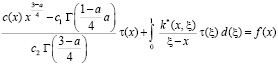, (16)

где

,

.

,

.

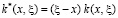
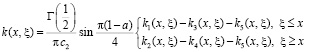
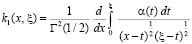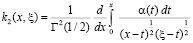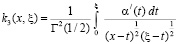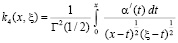Условие

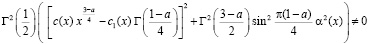
гарантирует существование регулятора [6], приводящего уравнение (16) к уравнению Фредгольма второго рода при

.

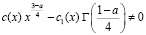Из возможности приведения задачи к эквивалентному интегральному уравнению Фредгольма второго рода и единственности искомого решения, следует существование решения поставленной задачи. По найденному 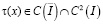определяются 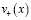, 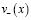по формулам (10), (11).

Решение задачи 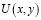в областях 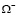и 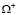находится как решение задачи Коши с данными , .

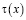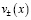Библиографическая ссылка