Строительство и эксплуатация инженерных объектов в криолитозоне осложняет ряд негативных факторов, одним из которых является зависимость механических свойств грунтов и дисперсных пород от температуры [1, 2]. Если в мерзлом состоянии грунты и породы обладают достаточной прочностью, то с повышением температуры прочность их существенно снижается. В общем случае, для характерных пород, эта зависимость близка к квадратичной [3, 4] в диапазоне отрицательных температур. Например, если температура мерзлых дисперсных горных пород повышается в четыре раза (с -4,0 °С до -1,0 °С), то прочность льдистого песчаника на сжатие уменьшается в два раза. При переходе из мерзлого состояния в талое отдельные виды дисперсных пород и льдистых грунтов полностью теряют свою несущую способность. Это не только осложняет эксплуатацию инженерных объектов (как наземных, так и подземных), но и может приводить к аварийным ситуациям и техногенным катастрофам [5–7]. Поэтому прогноз температурного режима грунтовых оснований поверхностных инженерных сооружений и дисперсных горных пород, вмещающих подземные и заглубленные сооружения, является актуальной задачей, позволяющей уже на стадии проектирования определить степень надежности принимаемых технических решений и оценить возможные риски при эксплуатации объектов в криолитозоне. При этом такие показатели, как глубина и скорость оттаивания грунтовых оснований и дисперсных пород, являются одними из основных при прогнозе теплового режима [8, 9]. Возможность управления этими показателями позволяет значительно снизить риски и повысить эксплуатационную надежность инженерных объектов криолитозоны. Известно, в частности, что эффективным способом управления глубиной оттаивания, наряду с применением специальных теплозащитных покрытий, является предварительное охлаждение горных пород вокруг подземного сооружения [10–12].
Целью настоящей работы была оценка влияния температурного фактора на скорость оттаивания дисперсных мерзлых горных пород. При этом рассматривается как естественная температура мерзлых пород, так и температура воздуха в сооружении.
Материалы и методы исследования
Для достижения цели воспользуемся методологией, изложенной нами ранее в работах [13–15], которая основана на использовании безразмерных критериев для нахождения искомых параметров. Исходным выражением для получения расчетных формул является условие Стефана, которое для двухфазной задачи может быть записано в виде
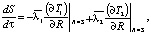 (1)
(1)
где
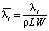 , (2)
, (2)
λi – коэффициент теплопроводности теплых (i = 1) и мерзлых (i = 2) пород, Вт/м·К; R – координата, м; S – глубина оттаивания пород, м; τ – время, с; ρ – плотность мерзлых пород, кг/м3; L – скрытая теплота плавления льда, Дж/кг (L = 335∙103 Дж/кг); W – льдистость пород, доли единицы; Ti – температура пород, °С (i = 1 – талых; i = 2 – мерзлых).
Рассмотрим для примера цилиндрическое подземное сооружение, размещенное в мерзлых дисперсных породах и эксплуатирующееся с положительной температурой воздуха. Примем распределение температуры в талой и мерзлой зоне квазистационарным, т.е.
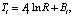
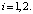 (3)
(3)
Для нахождения коэффициентов Ai и Bi воспользуемся следующими граничными условиями
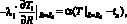 (4)
(4)
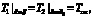 (5)
(5)
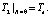 (6)
(6)
Здесь обозначены: Te – температура горных пород на глубине радиуса теплового влияния выработки, °C; δ – радиус теплового влияния, м; α – коэффициент теплопередачи от воздуха к поверхности, Вт/м2∙К; R0 – эквивалентный радиус выработки, м; tв – температура воздуха в выработке, °C.
Используя условия (4) и (5), найдем параметр A1:
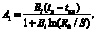 (7)
(7)
Где Bi – число Био, равное Bi = (αR0/λ1).
Термическое сопротивление теплозащитного слоя входит в параметр «α» и может быть определено по формуле [14].
RT = (δT/λT) = (1/ λ Bi) – 1/ɑ0 . (8)
Параметр A2 может быть найден из граничных условий (5) и (6).
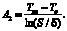 (9)
(9)
После несложных преобразований выражение (1) может быть представлено в безразмерном виде
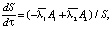 (10)
(10)
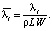
Если температура горных пород близка к температуре плавления льда, то A2 → 0 и скорость оттаивания пород будет равна
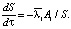 (11)
(11)
Выражение (11) позволяет определить степень влияния числа Био, характеризующего в данном случае термическое сопротивление теплозащитного слоя, на скорость оттаивания дисперсных пород.
Найдем функцию отношений скоростей оттаивания при разных начальных температурах горных пород, разделив выражение (10) на (11):
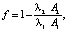 (12)
(12)
где
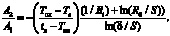 (13)
(13)
Окончательно, для определения соотношения скоростей оттаивания с учетом того, что температура в мерзлой зоне не равна Tпл и равна Tпл, получим
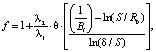 (14)
(14)
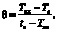
Анализ выражения (14) показывает, что оно не зависит от льдистости пород напрямую и определяется только соотношениями температур (tв/Te) и коэффициентов теплопроводности (λ2/λ1). В то же время сам параметр «S», входящий в формулу, зависит от льдистости, поэтому параметр «f» в общем случае является функцией критерия Стефана [15].
Для граничных условий первого рода (Bi → ∞), принимая температуру плавления льда, равной 0 °C, выражение (14) преобразуется к виду
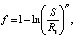
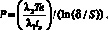 (15)
(15)
Результаты исследования и их обсуждение
Анализ выражения (15) показывает, что в начальный момент оттаивания S → R0 естественная температура горных пород не оказывает существенного влияния на скорость оттаивания (здесь необходимо учесть, что время начала оттаивания определяется отдельно для случая T ≠ Tпл). С ростом глубины оттаивания отношение уменьшается, что свидетельствует о возрастания влияния естественной температуры горных пород на процесс оттаивания. Однако, чем выше температура воздуха в выработке, тем это влияние меньше.
По полученным формулам были проведены вариантные расчеты, которые представлены в виде 3D графиков на рис. 1 и 2.
На рис. 1 показана зависимость параметра «f» от температуры воздуха в сооружении и естественной температуры горных пород. При этом принимались следующие характерные значения исходных данных: отношение коэффициентов теплопроводности мерзлых и талых пород – 1,2; отношение глубины ореола оттаивания к эквивалентному радиусу – 0,5 и 1,0. По оси «х» естественная температура горных пород приведена в абсолютных значениях.
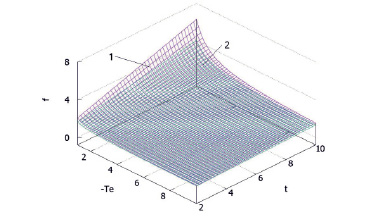
Рис. 1. Изменение скоростей оттаивания горных пород (f) в зависимости от их естественной температуры (Те, °С) и температуры воздуха в сооружении (t, °С): 1 – при h = Ro; 2 – при h = Ro/2
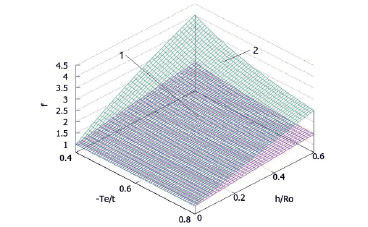
Рис. 2. Изменение скоростей оттаивания горных пород (f) в зависимости от безразмерной температуры (Te/t) и относительной глубины оттаивания (h/Ro): 1 – при (ƛ2/ ƛ1) = 4,0; 2 – при (ƛ2/ ƛ1) =1,2
Как видно из графиков на рисунке, с увеличением длительности периода оттаивания отношение скоростей оттаивания увеличивается: плоскость 1 находится выше плоскости 2. При этом качественный характер изменения параметра «f» практически не изменяется. С понижением естественной температуры значение его уменьшается. А при постоянной естественной температуре наблюдается сильная зависимость от температуры воздуха в сооружении. Причем чем выше естественная температура горных пород, тем эта зависимость сильнее. Об этом свидетельствует простое сравнение степени наклона плоскостей на рисунке, например, при температурах -2,0 °С и -8,0 °С.
На рис. 2 показана зависимость параметра «f», характеризующего отношения скоростей оттаивания пород при различной естественной температуре пород, в зависимости от безразмерного ореола оттаивания при различных теплофизических характеристиках (коэффициентов теплопроводности в мерзлом и талом состоянии). При этом для наглядности, в качестве сравнения, взято максимально возможное отношение коэффициентов теплопроводности пород в мерзлом и талом состоянии. То есть в качестве окружающих пород принят лед. В этом случае отношение равно 4. Для сравнения взят характерный вариант дисперсных пород с отношением коэффициентов теплопроводности в мерзлом и талом состоянии, равном 1, 2. При этом рассмотрен период, когда глубина ореола оттаивания изменяется от 0 (начало оттаивания) до 0,6 от эквивалентного радиуса выработки. Такой диапазон является характерным, например, для горных выработок рудников криолитозоны.
Как следует из рисунка, теплофизические свойства горных пород оказывают существенное влияние на изменение скорости оттаивания горных пород. Причем чем больше значение отношения коэффициентов теплопроводности пород в мерзлом и талом состоянии, тем эта зависимость сильнее.
Заключение
Сделана оценка влияния температурного фактора на скорость оттаивания дисперсных мерзлых горных пород, вмещающих подземное сооружение. Рассмотрено влияние как естественной температуры горных пород, так и температуры воздуха в подземном сооружении. Для обобщения полученных результатов использовался безразмерный температурный критерий, характеризующий отношение средней температуры воздуха за период оттаивания к начальной средней температуре мерзлых пород, вмещающих подземное сооружение. В качестве примера рассмотрен подземный объект с цилиндрической симметрией, размещенный в мерзлых дисперсных породах и эксплуатирующийся с положительной температурой воздуха. На основе приближенного решения двухфазной задачи Стефана для подземного объекта цилиндрической симметрии при граничных условиях третьего рода получены простые инженерные зависимости и разработан простой и понятный алгоритм оценки влияния естественной температуры мерзлых горных пород и температуры воздуха в сооружении на скорость оттаивания. Показано, что допущение о равенстве естественной температуры горных пород температуре плавления льда может существенно завышать скорость оттаивания в широком диапазоне исходных параметров. Причем, чем больше длительность процесса оттаивания, тем это отношение больше. Хотя по абсолютным значениям скорости оттаивания в обоих случаях уменьшаются с течением времени. В начальный момент оттаивания S → R0 естественная температура горных пород не оказывает существенного влияния на скорость оттаивания (здесь необходимо учесть, что время начала оттаивания определяется отдельно для случая T ≠ Tпл). С ростом глубины оттаивания отношение уменьшается, что свидетельствует о возрастания влияния естественной температуры горных пород на процесс оттаивания. Однако, чем выше температура воздуха в выработке, тем это влияние меньше. Дальнейшие исследования в данной области должны быть направлены на определение влияния естественной температуры горных пород на скорость оттаивания дисперсных горных пород вокруг сооружений различной симметрии.
Библиографическая ссылка
Галкин А.Ф. ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА СКОРОСТЬ ОТТАИВАНИЯ ДИСПЕРСНЫХ ПОРОД // Успехи современного естествознания. 2021. № 9. С. 26-30;URL: https://natural-sciences.ru/ru/article/view?id=37681 (дата обращения: 12.03.2026).
DOI: https://doi.org/10.17513/use.37681



