На сегодняшний день существуют различные методы спутникового позиционирования. Одним из перспективных является метод высокоточных координатных определений, или по-другому Precise Point Positioning (далее – РРР). Одной из проблем, ограничивающих его использование, является отсутствие рекомендаций по выполнению обработки по РРР-алгоритму с точки зрения продолжительности и количества принимаемых спутников [1]. В международном научном сообществе отсутствует регламентирующая документация по использованию данного метода. Помимо этого, в российском научном сообществе отсутствует точно выраженное определение РРР. Эти проблемы были подробно рассмотрены в работе [2].
На сегодняшний день обработка возможна по трем подходам: с использованием научного ПО, коммерческого ПО и интернет-сервисов [3; 4]. К первой группе относятся такие программные обеспечения, как Bernese, Grafnet. Ко второй группе можно отнести: Trimble Business Centre (далее – TBC), «КРЕДО ГНСС». Третья группа представлена интернет-сервисами: Trimble-RTX, CRSR, APPS, magicgnss, Auspos [5; 6].
В отличие от классических относительных методов, РРР-алгоритм не требует наличия базовых станций и реализуется благодаря использованию высокоточных данных, таких как высокоточные эфемериды, поправки к времени бортовых часов навигационных спутников, атмосферных поправок в пределе локальной области, влиянию приливных поправок смещения станции, вызванных солнечным и лунным притяжением; исключение затмений [7-8].
Цели исследования:
1. Выявить зависимость продолжительности измерений на точность получения координат в случае обработки по РРР-алгоритму.
2. Оценить влияние факторов, влияющих на точность определения координат при РРР-алгоритме (косвенно оценить количество спутников; продолжительность измерений; расстояния между пунктами).
3. Исследовать точность получения координат при уравнивании данных по РРР-алгоритму и статике.
Материалы и методы исследования
Для решения основных задач исследования была сформирована спутниковая сеть, состоящая из 5 пунктов. RINEX-файлы, как и эталонные координаты пунктов (LOBN, ODIN, ZHDR, HGNK), были получены из сети базовых станций EFT COORS [9; 10]. Данные по 5 пункту были получены самостоятельно. В качестве исходного (опорного) пункта был выбран пункт МИИТ. На рисунке 1 представлена данная сеть.
В дальнейшем происходила камеральная обработка сети с использованием РРР-алгоритма. Для обработки по РРР-алгоритму были применены интернет-сервисы Trimble RTX и CRSR. Для контроля данных, получаемых в ходе обработки с использованием интернет-сервисов, была также выполнена и обработка в статике с использованием программного обеспечения «КРЕДО ГНСС» версии 2.0.
В дальнейшем в статике была выполнена обработка базовых векторов с использованием высокоточных эфемерид, т.е. были получены «обработанные» приращения координат между пунктами. В случае обработки по РРР-алгоритму приращения координат были вычислены вручную с использованием ПО Microsoft Excel.
После получения приращений координат с использованием РРР-алгоритма и статики было выполнено уравнивание данной сети. Уравнение поправок в этом случае будет выглядеть стандартным образом по формуле [11]:
AD + L = V,
где D – вектор оценок искомых неизвестных (поправки к координатам);
А – матрица коэффициентов параметрического уравнивания;
L – вектор невязок, между приращениями координат.
Результаты обработки в статике приведены в таблице 1.
Результаты исследования и их обсуждение
В таблицах 1-3 приводятся разности приращений координат после уравнивания.
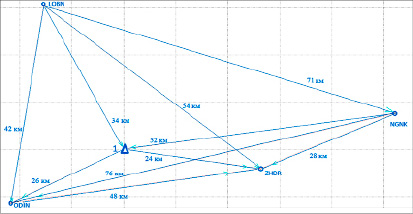
Рис. 1. Схема спутниковой сети
Таблица 1
Разности приращений координат после уравнивания при 1 часе
|
Линия |
Уравнивание в статике |
Уравнивание РРР-RTX |
Уравнивание РРР-CRSR |
||||||
|
δX,м |
δY,м |
δZ,м |
δX,м |
δY,м |
δZ,м |
δX,м |
δY,м |
δZ,м |
|
|
LOBN-NGNK |
-0,050 |
-0,007 |
-0,012 |
0,014 |
0,001 |
-0,005 |
0,007 |
-0,006 |
-0,018 |
|
LOBN-ODIN |
-0,085 |
-0,010 |
-0,020 |
0,018 |
0,007 |
0,015 |
0,018 |
0,008 |
0,014 |
|
LOBN-ZHDR |
-0,012 |
0,024 |
0,016 |
-0,010 |
-0,001 |
-0,002 |
-0,003 |
0,004 |
0,001 |
|
LOBN-1 |
0,061 |
0,008 |
0,107 |
0,061 |
-0,015 |
0,170 |
-0,062 |
-0,047 |
-0,002 |
|
NGNK-ODIN |
0,056 |
0,077 |
0,028 |
0,004 |
0,006 |
0,020 |
0,011 |
0,014 |
0,032 |
|
NGNK-ZHDR |
0,065 |
-0,023 |
0,020 |
-0,024 |
-0,002 |
0,002 |
-0,010 |
0,011 |
0,018 |
|
NGNK-1 |
0,080 |
0,061 |
0,109 |
0,047 |
-0,016 |
0,175 |
-0,069 |
-0,041 |
0,016 |
|
ODIN-ZHDR |
0,074 |
0,034 |
0,036 |
-0,028 |
-0,008 |
-0,017 |
-0,021 |
-0,003 |
-0,013 |
|
1-ODIN |
-0,124 |
-0,064 |
-0,017 |
-0,043 |
0,022 |
-0,155 |
0,080 |
0,055 |
0,016 |
|
1-ZHDR |
-0,050 |
-0,030 |
-0,081 |
-0,071 |
0,014 |
-0,172 |
0,059 |
0,052 |
0,003 |
Таблица 2
Разности приращений координат после уравнивания при 2 часах
|
Линия |
Уравнивание в статике |
Уравнивание РРР-RTX |
Уравнивание РРР-CRSR |
||||||
|
δX,м |
δY,м |
δZ,м |
δX,м |
δY,м |
δZ,м |
δX,м |
δY,м |
δZ,м |
|
|
LOBN-NGNK |
0,022 |
-0,046 |
0,032 |
0,023 |
0,008 |
0,001 |
0,022 |
0,009 |
0,000 |
|
LOBN-ODIN |
-0,063 |
-0,040 |
-0,039 |
0,022 |
0,013 |
0,022 |
0,023 |
0,013 |
0,022 |
|
LOBN-ZHDR |
0,040 |
-0,020 |
0,036 |
0,001 |
0,008 |
0,011 |
-0,006 |
0,005 |
0,001 |
|
LOBN-1 |
0,070 |
0,029 |
0,109 |
0,027 |
-0,035 |
0,114 |
-0,101 |
-0,090 |
-0,118 |
|
NGNK-ODIN |
-0,036 |
0,049 |
-0,030 |
-0,001 |
0,005 |
0,021 |
0,001 |
0,004 |
0,022 |
|
NGNK-ZHDR |
0,001 |
0,016 |
-0,003 |
-0,022 |
0,001 |
0,009 |
-0,028 |
-0,003 |
0,000 |
|
NGNK-1 |
0,051 |
0,082 |
0,070 |
0,004 |
-0,043 |
0,113 |
-0,123 |
-0,099 |
-0,118 |
|
ODIN-ZHDR |
0,103 |
0,021 |
0,075 |
-0,021 |
-0,004 |
-0,011 |
-0,029 |
-0,007 |
-0,021 |
|
1-ODIN |
-0,136 |
-0,077 |
-0,141 |
-0,005 |
0,048 |
-0,092 |
0,124 |
0,103 |
0,140 |
|
1-ZHDR |
-0,032 |
-0,056 |
-0,066 |
-0,026 |
0,044 |
-0,103 |
0,095 |
0,096 |
0,119 |
Таблица 3
Разности приращений координат после уравнивания при 3 часах
|
Линия |
Уравнивание в статике |
Уравнивание РРР-RTX |
Уравнивание РРР-CRSR |
||||||
|
δX,м |
δY,м |
δZ,м |
δX,м |
δY,м |
δZ,м |
δX,м |
δY,м |
δZ,м |
|
|
LOBN-NGNK |
0,021 |
-0,041 |
0,032 |
0,016 |
0,005 |
-0,003 |
0,018 |
0,006 |
0,002 |
|
LOBN-ODIN |
-0,048 |
-0,032 |
-0,010 |
0,019 |
0,009 |
0,020 |
0,019 |
0,010 |
0,020 |
|
LOBN-ZHDR |
0,022 |
-0,021 |
0,029 |
-0,007 |
0,002 |
0,002 |
-0,005 |
0,004 |
0,006 |
|
LOBN-1 |
0,073 |
0,035 |
0,109 |
0,014 |
-0,067 |
0,103 |
-0,103 |
-0,092 |
-0,139 |
|
NGNK-ODIN |
-0,039 |
0,042 |
-0,017 |
0,003 |
0,004 |
0,023 |
0,001 |
0,004 |
0,019 |
|
NGNK-ZHDR |
0,002 |
0,004 |
-0,004 |
-0,023 |
-0,002 |
0,004 |
-0,023 |
-0,001 |
0,004 |
|
NGNK-1 |
0,050 |
0,085 |
0,072 |
-0,002 |
-0,072 |
0,106 |
-0,121 |
-0,098 |
-0,140 |
|
ODIN-ZHDR |
0,069 |
0,011 |
0,038 |
-0,026 |
-0,006 |
-0,018 |
-0,024 |
-0,005 |
-0,014 |
|
1-ODIN |
-0,118 |
-0,076 |
-0,114 |
0,005 |
0,076 |
-0,083 |
0,122 |
0,102 |
0,159 |
|
1-ZHDR |
-0,049 |
-0,065 |
-0,076 |
-0,021 |
0,070 |
-0,101 |
0,098 |
0,097 |
0,145 |
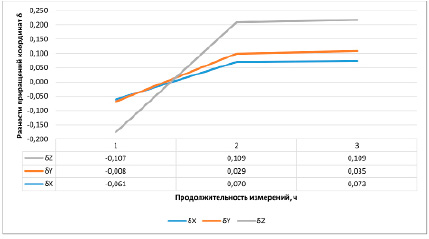
Рис. 2. Влияние продолжительности измерений на получаемые результаты при уравнивании статических данных
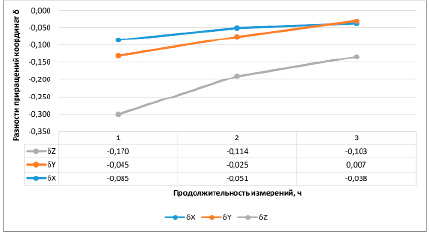
Рис. 3. Влияние продолжительности измерений на получаемые результаты при уравнивании RTX-данных
При сравнении таблиц 1-3 можно заметить, что разности приращений координат в сравнении RTX и CRSR отличаются на небольшие величины (1-2 мм в случае, если оба пункта относились к EFT).
На рисунке 2 приведен график, иллюстрирующий влияние продолжительности измерений на получаемые результаты. На рисунках 3, 4 приводятся данные по РРР-алгоритму.
Однако при анализе таблиц 1-3 можно заметить, что разности приращений координат на линиях LOBN-1, NGNK-1, 1-ODIN, 1-ZHDR отличаются на max 12 см по модулю, из-за влияния PDOP-фактора.
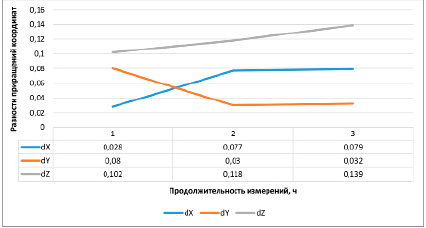
Рис. 4. Влияние продолжительности измерений на получаемые результаты при уравнивании CRSR-данных
DOP (dilution of precision) – термин, характеризующий пространственное положение спутников относительно антенны приемника. В настоящее время существует большое количество DOP-факторов, однако наиболее подходящий PDOP-фактор
PDOP (position DOP) – снижение точности по местоположению. При этом точность PDOP-фактора зависит от таких составляющих, как HDOP (точность в горизонтальной плоскости); VDOP (точность в вертикальной плоскости); средняя величина PDOP-фактора варьировалась от 1.2 и до 1.6 на станциях LOBN, NGNK, ODIN, ZHDR.
В случае станции 1 (MIIT) PDOP-фактор при одном часе составил 1.6*(20 спутников 6Rи 14G); при двух – 1.9** (23 спутника (7R и 13G)); при трех – 1.5*** (23 спутника (11R и 17G). Ниже приведены некоторые комментарии по изменению PDOP-фактора:
*c 11:01:18 до 11:02:25 колебался с 3.0 до 7.0, после чего упал до 1.8;
**с 11:19:42 до 11:19:39 1.7, c 11:19:39 по 11:20:48 5.45, до 11:30 5.64, после чего с 11:20:51 не превышал 1.9;
*** до 11:19:36 PDOP не превышал 1.3, после чего до 11:20:29 варьировался от 1.3 до 4.9, затем подъем до 11:20:38, когда значение PDOP составило 21.8, после чего спуск до 11:20:49 до значения PDOP 1.5.
Считается, в том случае, когда PDOP «2-3» – точность «отличная», когда «4-6» – точность хорошая.
Из данных абзацев сделан вывод о том, что при одинаковом количестве используемых спутников для обработки по РРР-алгоритму величина PDOP-фактора играет ключевую роль, поскольку происходит отягощение результатов наблюдений.
В работах [12; 13] рассматривается возможность применения РРР-алгоритма для решения таких задач, как решение геодинамических задач, с целью возможного контроля за сейсмически активными регионами с целью прогнозирования возможных землетрясений. В работе [14] рассматривается возможность применения РРР-алгоритма спутниковых данных для решения геодезических задач, в части построения геодезических сетей.
Выводы
В ходе анализа выполненных работ получены следующие основные выводы.
1. В диапазоне расстояний (24-76 км) точность взаимного определения координат геодезических пунктов примерно сопоставима между собой.
2. Точность определения координат практически неизменна свыше 2 часов (таблицы 1-3).
3. Колебания PDOP-фактора оказывают большое влияние (практически в 5 раз) на получаемые результаты как в статике, так и по РРР-алгоритму.
4. Точность уравнивания по РРР-алгоритму несколько выше, чем при уравнивании данных, полученных в статике.
Библиографическая ссылка
Макаров С.О., Тихонов А.Д. АНАЛИЗ ТОЧНОСТИ КООРДИНАТ ГЕОДЕЗИЧЕСКИХ ПУНКТОВ, ОПРЕДЕЛЕННЫХ С ПОМОЩЬЮ МЕТОДИКИ ВЫСОКОТОЧНЫХ ООРДИНАТНЫХ ОПРЕДЕЛЕНИЙ ОБРАБОТКИ СПУТНИКОВЫХ ДАННЫХ // Успехи современного естествознания. 2023. № 1. С. 94-99;URL: https://natural-sciences.ru/ru/article/view?id=37990 (дата обращения: 07.01.2026).
DOI: https://doi.org/10.17513/use.37990



