Введение
Для районов многолетнемерзлых грунтов вопросы сохранения мерзлого состояния и несущей способности грунтовых оснований инженерных сооружений всегда имеют особую важность. Актуально это и для автомобильных дорог как для протяженных линейных объектов, проходящих через участки различных геологических и геокриологических условий. При этом основным определяющим критерием устойчивости является стабильный температурный режим с сохранением мерзлого состояния грунтовых оснований. Во избежание дальнейших проблем с эксплуатацией сооружений необходимо выполнять численное моделирование теплового режима грунтового основания и прогнозную оценку его устойчивости [1].
Для прогнозной оценки состояния грунта основания, насыпи и откосов асфальтовой автодороги в среде численного мультифизического моделирования Comsol была разработана и реализована модель системы «автодорога – грунт – атмосфера», учитывающая фазовые переходы поровой влаги, сезонные колебания температуры воздуха, изменения скорости ветра, приток тепла за счет солнечной радиации с учетом отражающей способности поверхностей, влияние сезонного снегового покрова и его профиль в результате регулярной очистки автодороги от снега.
Цель работы – дать прогнозную оценку состояния грунта основания асфальтовой автодороги на период ее эксплуатации в условиях многолетнемерзлых грунтов Якутии.
Материалы и методы исследования
Исследование температурного состояния грунтов оснований автодороги проводилось методами математического моделирования с решением методом конечных элементов.
Постановка математической модели переноса тепла в теле насыпи автодороги и грунтов оснований описывается уравнением теплопроводности с фазовыми переходами в спектре температур (1) с соответствующими начальным (2) и граничными условиями (3).
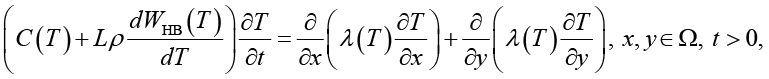 (1)
(1)
 (2)
(2)
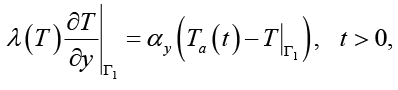 (3)
(3)
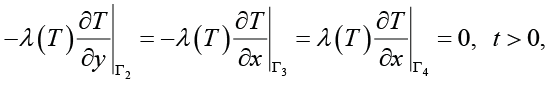 (4)
(4)
где С(Т) и λ(Т) – соответственно, объемная теплоемкость, Дж/ (м3∙ºC) и теплопроводность строительных материалов, насыпи и грунтов оснований, Вт/(м∙ºC); L – скрытая теплота фазового перехода вода-лед, Дж/кг; ρ – плотность скелета дисперсного материала, кг/м3; WHB(Т) – функция незамерзшей воды, кг/кг; T0(y) – начальный профиль температуры по глубине массива насыпи и грунтов оснований, ºC; αy – эффективный коэффициент теплоотдачи, Вт/(м2∙ºC); Ta(t) – температура атмосферного воздуха, ºC.
Постановка такой задачи теплопроводности для промерзающих-протаивающих влажных дисперсных материалов, коими являются дорожная полотно, насыпь и грунты основания, отличается от традиционной постановки задачи Стефана [2, с. 358] тем, что вместо дельта-функции Дирака, характеризующей интенсивность фазовых переходов в объемной теплоемкости, стоит производная от функции незамерзшей воды по температуре. Таким образом, производится «естественное сглаживание» функций теплопроводности и объемной теплоемкости влажных дисперсных материалов.
Область Ω с соответствующими границами от Г1 до Г4, в которой отыскивается решение поставленной задачи, имеет следующий вид (рис. 1).
Как видно, входящие в уравнение теплопроводности коэффициенты представляют собой теплофизические свойства отдельных слоев, слагающих дорожное полотно, насыпь и грунты основания, которые зависят от температуры. Объемная теплоемкость в случае промерзания или протаивания становится эффективной и содержит скрытую теплоту фазового превращения воды в лед. Данная задача нелинейна из-за зависимости теплофизических свойств дисперсных грунтов от температуры и наличия фазовых переходов, происходящих в спектре температур, поэтому решение такой задачи возможно получить только численно. Для решения нелинейной задачи теплопроводности можно применить метод конечных разностей или метод конечных элементов. Последний в данном случае будет эффективным, так как область, где отыскивается температурное поле, представляет собой сложную геометрию, при дискретизации которой получаются нерегулярные узлы.
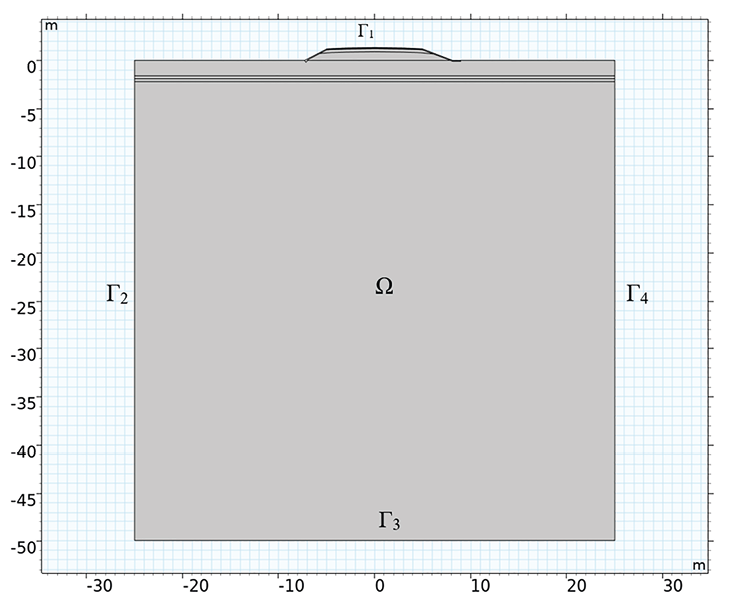
Рис. 1. Расчетная область Примечание: сформировано авторами по результатам данного исследования
Таблица 1
Физические и теплофизические свойства материалов дорожного покрытия, насыпи и грунтов основания (г. Якутск)
|
Вид слоя |
L, м |
ρ, кг/м3 |
W, д.е. |
Ip, д.е. |
Wp, д.е. |
λth , W/(m*K) |
λf , W/(m*K) |
Cth∙106, J/(m3*K) |
Cth∙106, J/(m3*K) |
Tbf , °C |
|
Асфальтобетон плотный |
0,05 |
2400 |
- |
- |
- |
1,4 |
1,4 |
3,12 |
3,12 |
- |
|
Асфальтобетон пористый |
0,07 |
2300 |
- |
- |
- |
1,25 |
1,25 |
3,22 |
3,22 |
- |
|
Щебень |
0,31 |
1800 |
0,05 |
- |
- |
1,39 |
1,48 |
2,4 |
2,22 |
0,0 |
|
Грунт земляного полотна (песок средней крупности) |
0,9 |
1550 |
0,22 |
- |
- |
2,14 |
2,38 |
2,85 |
2,15 |
-0,6 |
|
Суглинок легкий пылеватый, засоленный |
1,6 |
1370 |
0,31 |
0,09 |
0,25 |
1,48 |
1,59 |
3,07 |
2,2 |
-1,0 |
|
Песок мелкий, засоленный |
0,6 |
1460 |
0,25 |
- |
- |
2,09 |
2,32 |
2,87 |
2,14 |
-0,5 (-0,24) |
|
Песок средней крупности |
11,9 |
1520 |
0,23 |
- |
- |
2,13 |
2,37 |
2,86 |
2,15 |
-0,12 |
Примечание: составлено авторами на основе полученных данных в ходе исследования, а также источника [5].
Поставленная задача решалась методом конечных элементов в программе СОМSОL Multiphysics. Выбор этого программного пакета обусловлен его широкими возможностями, в первую очередь гибкостью задания вида уравнения переноса тепла, граничных условий, возможностью настройки и реализации различного уровня сложности математических функций, а также задания пользователем своих уравнений или их систем. Сравнение СОМSОL Multiphysics c альтернативными программными приложениями для моделирования методом конечных элементов показывает, что оно ни в чем им не уступает, и более того, обладает определенными преимуществами [3; 4].
Теплофизические свойства слоев, слагающих дорожное полотно, насыпь и грунты основания, определялись по справочным таблицам для строительных материалов и из СП 25.13330.2020 «Основания и фундаменты на вечномерзлых грунтах» [5]. В этом своде правил приводятся формулы для определения температуры начала замерзания грунтов, расчета засоленности, объемных теплоемкостей в талом и мерзлом состояниях, а также таблицы и формулы для теплопроводностей в этих же состояниях. Для учета фазовых превращений поровой воды в лед и обратно в этом же своде имеются таблицы и формула для расчета количества незамерзшей воды. При построении функции незамерзшей воды на основе расчетных значений количества незамерзшей воды от температуры применялась аппроксимация, предложенная в работе [6, с. 18; 7, с. 41]. Основные данные по структуре грунта для модели взяты из таблиц инженерных изысканий и приведены в таблице 1.
В граничное условие (3) теплообмена с атмосферным воздухом входит температура воздуха в зависимости от времени. Данная величина должна иметь поправку на температуру за счет воздействия солнечной радиации. Оценка среднемесячной температуры поверхности дорожной насыпи производилась с привлечением нормативных документов СП 498.1325800.2020 «Основания и фундаменты зданий и сооружений на многолетнемерзлых грунтах. Требование к инженерной подготовке территории» [8] и СП 447.1325800.2019 «Железные дороги в районах вечной мерзлоты» [9]. Для естественной поверхности грунта воздействие солнечной радиации согласно [9], п. 7, приложение А
T(t) = Ta(t) + ΔTr + ΔTε, (5)
где Ta(t) – среднемесячная температура атмосферного воздуха, приведенная в таблице 2, ΔTr и ΔTε – поправки на теплообмен за счет солнечной радиации и испарения, ºC.
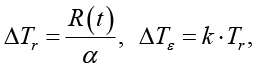 (6)
(6)
где α – коэффициент теплообмена, Вт/(м2∙ºC); R(t) – радиационный баланс различных поверхностей, Вт/м2; k – коэффициент, учитывающий характер поверхности. В первом приближении равный для естественной поверхности – 0,8, а для оголенной – 0,3.
Для определения коэффициента теплообмена в зависимости от скорости ветра использовалась широко применяемая формула Юргенса [10; 11]:
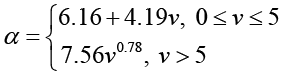 (7)
(7)
Радиационный баланс для различных поверхностей регламентируется в п. 5.2.13 СП 498.1325800.2020 [12].
Таблица 2
Климат (среднемесячные значения температуры воздуха, скорости ветра и солнечной радиации) (г. Якутск)
|
Параметр |
Январь |
Февраль |
Март |
Апрель |
Май |
Июнь |
|
Ta, ºC |
-39,1 |
-34,6 |
-20,3 |
-4,7 |
7,5 |
16,2 |
|
v, м/с |
1,1 |
1,1 |
1,7 |
2,6 |
3,1 |
2,9 |
|
Qc, Вт/м2 |
12,69 |
47,12 |
122,83 |
196,37 |
220,65 |
253,86 |
|
Параметр |
Июль |
Август |
Сентябрь |
Октябрь |
Ноябрь |
Декабрь |
|
Ta, ºC |
19,3 |
15,2 |
5,9 |
-7,8 |
-27,8 |
-37,8 |
|
v, м/с |
2,6 |
2,5 |
2,4 |
2,2 |
1,6 |
1,1 |
|
Qc, Вт/м2 |
234,09 |
175,10 |
109,18 |
52,64 |
20,83 |
6,72 |
Примечание: составлено авторами на основе источника [12].
Таблица 3
Высота и средняя плотность снежного покрова (г. Якутск)
|
Параметр |
Октябрь |
Ноябрь |
Декабрь |
Январь |
||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
|
|
Hs, м |
0,01 |
0,05 |
0,08 |
0,10 |
0,19 |
0,19 |
0,19 |
0,22 |
0,24 |
0,24 |
0,24 |
0,24 |
|
ρs, г/см3 |
0,08 |
0,10 |
0,12 |
0,12 |
0,12 |
0,14 |
0,15 |
0,15 |
0,15 |
0,16 |
0,16 |
0,16 |
|
Параметр |
Февраль |
Март |
Апрель |
|||||||||
|
1 |
2 |
3 |
1 |
2 |
3 |
1 |
2 |
3 |
||||
|
Hs, м |
0,25 |
0,25 |
0,25 |
0,26 |
0,24 |
0,24 |
0,18 |
0,06 |
– |
|||
|
ρs, г/см3 |
0,16 |
0,17 |
0,18 |
0,18 |
0,19 |
0,19 |
0,22 |
0,20 |
– |
|||
Примечание: составлено авторами на основе источника [12].
Таблица 4
Полевые данные замеров температур по глубине (15 мая 2023 г.)
|
z, м |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
T0, ºC |
-0.2 |
-0.3 |
-0.4 |
-0.6 |
-0.6 |
-0.8 |
-0.8 |
|
z, м |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
T0, ºC |
-0.9 |
-1.0 |
-1.1 |
-1.1 |
-1.2 |
-1.1 |
-1.2 |
Примечание: составлено авторами на основе полученных данных в ходе исследования.
Так, для песчаных, щебеночных и асфальтовых поверхностей R(t) определяется по формуле:
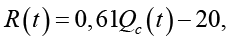 (8)
(8)
а для бетонных и железобетонных поверхностей:
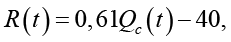 (9)
(9)
где Qc(t) – суммарная солнечная радиация, приведенная в таблице 2 и определяемая согласно документу СП 131.13330 «Строительная климатология» [12].
В модели предполагается, что поверхность асфальта в зимний период не имеет снежного покрова, поэтому температурные поправки учитываются на все месяцы, остальные поверхности, такие как естественный грунт и оба откоса дорожной насыпи, поправки на температуру воздуха, учитываются только с мая по октябрь.
Коэффициент теплопередачи от холодного воздуха к поверхности снежного покрова через его толщу к поверхности грунта или поверхности насыпи, как в работах [13; 14], определяется по формуле:
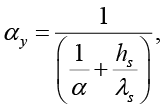 (10)
(10)
где hs – высота снежного покрова, приведенная в таблице 3 и определяемая по данным ближайшей станции по метеонаблюдениям, м; λs – теплопроводность снега, Вт/(м∙ºC).
Теплопроводность снежного покрова рассчитывалась по формуле, предложенной Б.В. Проскуряковым [15]:
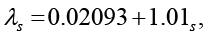 (11)
(11)
где s – плотность снега, значения приводятся в таблице 3.
Замеры начального профиля температур слоев грунтового массива проводятся изыскательской организацией. Для этого проводится обустройство температурной скважины глубиной до 15 м, путем бурения и далее установки термотрубки с размещением в ней термокос из датчиков температур (логгеров). Замер температур по глубине проводится с шагом в 1 метр. Данные по начальному распределению температуры по глубине массива приведены в таблице 4.
Результаты исследования и их обсуждение
В результате численного моделирования получены прогнозные значения температур автодорожного полотна насыпи и грунтов оснований за счет теплообмена с наружным атмосферным воздухом для различных моментов времени.
Распределение температур по глубине массива в начальный момент времени (рис. 2) имело растепленный характер из-за возведения насыпи в зимний период.
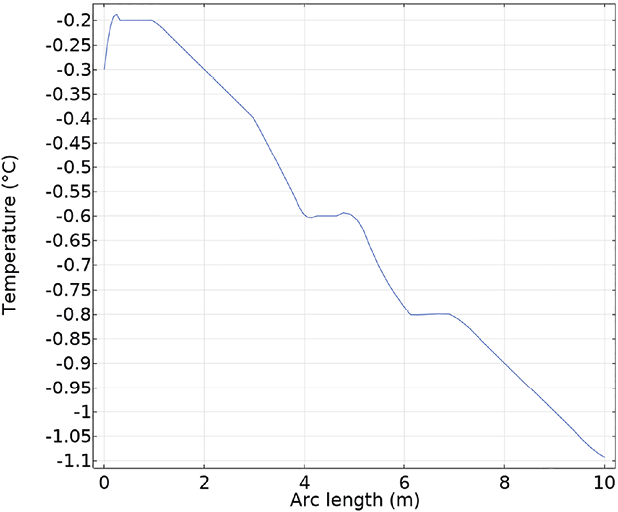
Рис. 2. Профиль распределения температуры по глубине на начальный момент времени (15.05.2023 г.) Примечание: составлено авторами по результатам данного исследования
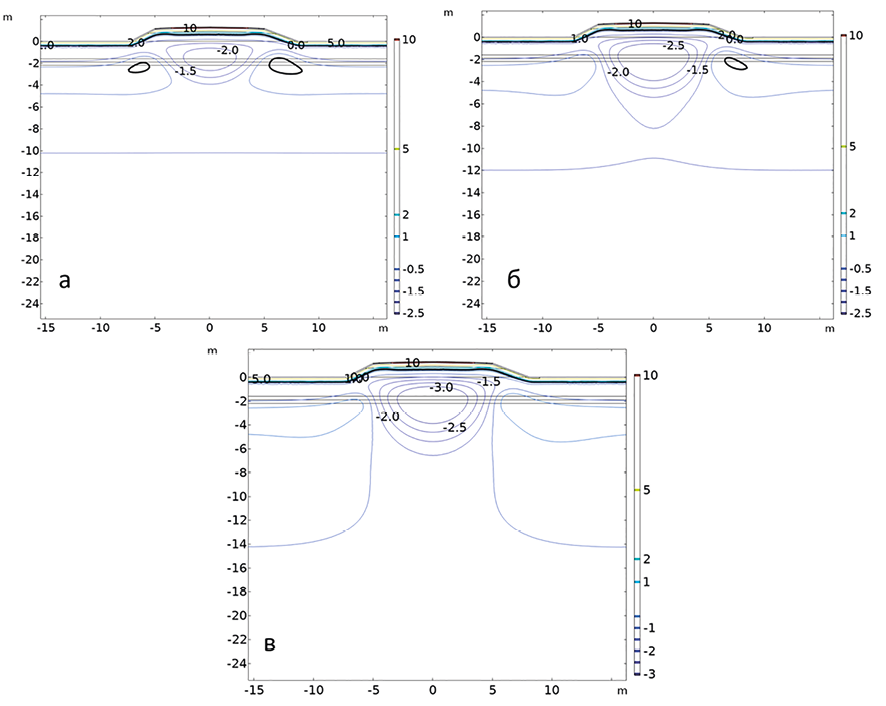
Рис. 3. Конфигурации изотерм: а) через 2 года; б) через 5 лет; в) через 10 лет Жирной черной линией обозначены нулевые изотермы Примечание: составлено авторами по результатам данного исследования
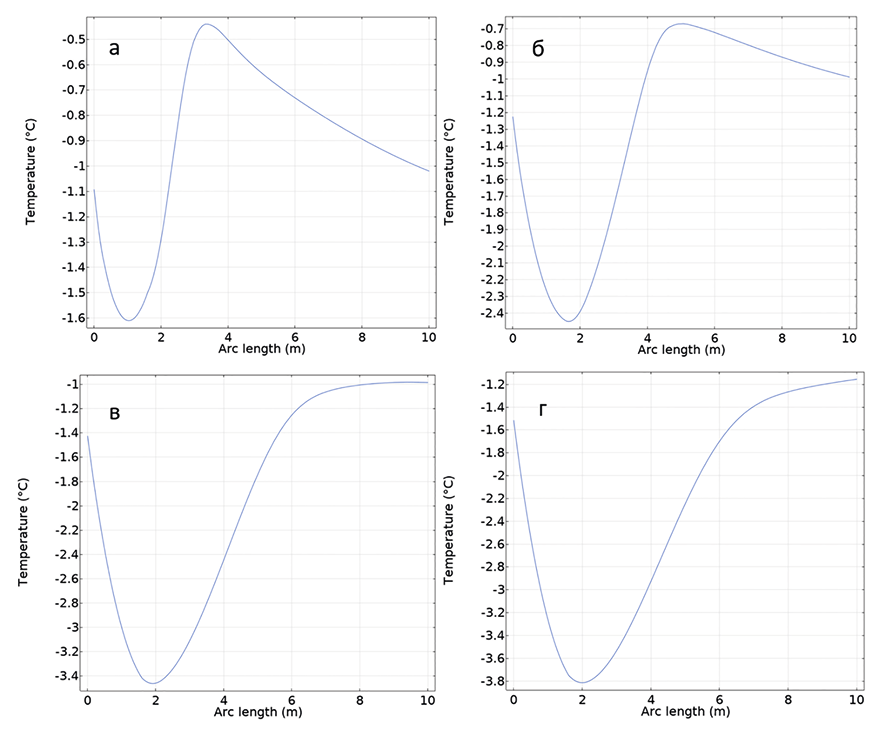
Рис. 4. Профили распределения температуры по глубине: а) через 1 год; б) через 2 года; в) через 5 лет; г) через 10 лет Примечание: составлено авторами по результатам данного исследования
Анализ полученных изотерм (рис. 3) показывает, что после первого расчетного года формируется ядро промерзания под насыпью с постепенным понижением температур в последующие годы.
Характер распределения температур по глубине массива, начиная с первого расчетного года, изменяется в сторону отрицательных значений (рис. 4).
Температура на глубине нулевых амплитуд (10 м) в начале расчетов немного повышается, за первые три года достигая -0,96 ºC, а затем в последующие годы уменьшается, доходя до значения -1,15 ºC на десятом году. Повышение температуры на начальном периоде объясняется отложенным влиянием растепления верхних слоев грунта в процессе строительных работ.
Все графики распределения температур представлены для середины мая, т.к. исходная точка моделирования – 15 мая 2023 года. При этом минимум температуры в середине мая смещается с глубины 1 метр со значением -1,6 ºC в первый год на глубину 2 метра со значением -3,8 ºC через 10 лет.
Полученный характер изменения температурного режима грунта после строительства автодороги с понижением значений температуры – следствие изменения профиля грунта с обустройством насыпи, а также регулярной расчистки с поверхности автодороги снегового покрова, имеющего теплоизолирующие свойства для подстилающих поверхностей.
Заключение
В результате проведенного исследования разработана и реализована математическая модель, позволяющая осуществлять прогнозный расчет температурного режима автодороги с учетом фазовых переходов поровой влаги, сезонных колебаний температуры воздуха, изменения скорости ветра, притока тепла к поверхности за счет солнечной радиации с учетом отражающей способности поверхностей, влияния сезонного снегового покрова и его профиля в результате регулярной очистки автодороги от снега.
Результаты проведенного численного моделирования дают прогнозную оценку на постепенное охлаждение и стабильное мерзлое состояние грунтового основания и насыпи автомобильной дороги на период эксплуатации в 10 лет при условии отсутствия влияющих на тепловой режим нештатных ситуаций (изменение грунтовых условий, переувлажнение и заболачивание территории, разрушение участка автодороги и прочие нарушения эксплуатации).
Конфликт интересов
Библиографическая ссылка
Малышев А.В., Тимофеев А.М., Большев К.Н., Цеева А.Н. МОДЕЛИРОВАНИЕ ТЕМПЕРАТУРНОГО РЕЖИМА НАСЫПИ АВТОДОРОГИ И ГРУНТОВ ОСНОВАНИЙ В УСЛОВИЯХ МНОГОЛЕТНЕЙ МЕРЗЛОТЫ ЯКУТИИ // Успехи современного естествознания. 2025. № 11. С. 71-78;URL: https://natural-sciences.ru/ru/article/view?id=38454 (дата обращения: 12.03.2026).
DOI: https://doi.org/10.17513/use.38454



