Существуют различные виды формул для расчета линий тренда (достоверности) аппроксимации.
Для аппроксимации данных по методу наименьших квадратов используются следующие виды уравнений [2], [4], [5]:
– Линейная –
y = mx + b, (1)
где m – угол наклона и b – координата пересечения оси абсцисс;
– Полиномиальная –
y = b + c1x + c2x2 + c3x3 + …+ c6x6, (2)
где b и с1 … с6 – константы;
– Логарифмическая –
y = cln x + b, (3)
где с и b – константы, ln – функция натурального логарифма;
– Экспоненциальная –
y = cebx, (4)
где с и b – константы, е – основание натурального логарифма;
– Степенная –
y = cxx, (5)
где с и b – константы.
Линии тренда обычно используются в задачах прогнозирования. Такие задачи решают с помощью методов регрессионного анализа. С помощью регрессионного анализа можно продолжить линию тренда вперед или назад, экстраполировать ее за пределы, в которых данные уже известны, и показать тенденцию их изменения. Можно также построить линию скользящего среднего, которая сглаживает случайные флуктуации, яснее демонстрирует модель и прослеживает тенденцию изменения данных.
Линиями тренда можно дополнить ряды данных, представленные на ненормированных плоских диаграммах с областями, линейчатых диаграммах, гистограммах, графиках, биржевых, точечных и пузырьковых диаграммах. Нельзя дополнить линиями тренда ряды данных на объемных диаграммах, нормированных диаграммах, лепестковых диаграммах, круговых и кольцевых диаграммах. При замене типа диаграммы на один из вышеперечисленных соответствующие данным линии тренда будут потеряны.
После того как уравнение регрессии найдено, необходимо произвести статистический анализ результатов. Этот анализ заключается в проверке значимости всех коэффициентов регрессии в сравнении с ошибкой воспроизводимости и адекватности уравнения. Такое исследование называется регрессивным анализом. Примем при проведении регрессивного анализа следующие допущения [2], [3], [5]:
1. Входной параметр х измеряется с пренебрежимо малой ошибкой по сравнению с ошибкой в определении у. Большая ошибка у объясняется наличием в каждом процессе не выявленных переменных, не вошедших в уравнение регрессии.
2. Результаты наблюдений у1, у2, …, уn, над выходной величиной у представляют собой независимые нормально распределенные случайные величины.
3. При проведении эксперимента с объемом выборки n при условии, что каждый опыт повторен m раз, i = 1, 2, …, n, выборочные дисперсии 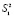 ,
, 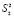 , …
, … 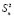 должны быть однородны.
должны быть однородны.
При одинаковом числе параллельных опытов проверка однородности дисперсии сводится к следующему [2], [3], [5]:
1. Ввод экспериментальных данных х и у в таблицу 1.
2. Используя табличные данные, строим график зависимости х и у.
3. Строим линию тренда, используя точки графика.
При построении линии тренда (аппроксимации) укажем:
– тип линии уравнения;
– степень в диапазоне от 2÷6;
– показать уравнение на диаграмме;
– поместить на диаграмму величину достоверности аппроксимации (R2)
Величина достоверности аппроксимации R2[1], [4]:
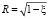 , (6)
, (6)
или
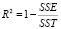 , (7)
, (7)
где
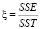 , (8)
, (8)
ξ – сила связи между х и у (дисперсионное отношение по Фишеру) [2], [3]:
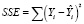 –
–
остаточная дисперсия; (9)
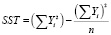 –
–
общая дисперсия. (10)
Связь тем сильнее, чем меньше ξ.
Чем больше R2, тем сильнее связь [2], [3], следовательно, уравнение регрессии адекватно эксперименту.
0 ≤ R ≤ 1. (11)
Если R = 1, то существует функциональная зависимость между, параметрами.
Однако при R = 0 величины х и у нельзя считать независимыми, так как связь между ними, не сказываясь на дисперсиях, может проявить себя в моментах более высокого порядка. И только при нормальном распределении равенство нулю корреляционного отношения однозначно свидетельствует об отсутствии связи между случайными величинами. Корреляционное отношение, как и коэффициент корреляции в линейной регрессии, характеризует тесноту связи между случайными величинами. Вообще анализ силы связи по R называют корреляционным анализом.
Зависимость производительности (G) барабанного агрегата от скорости теплоносителя (ϑвх) на входе и угла наклона барабана (α)
|
№ п/п |
Число оборотов барабана п, об/мин |
Скорость сушильного агента на входе в барабан, ϑвх, м/с |
Угол наклона барабана, αо |
Производительность, Gі∙10-3, кг/с |
Производительность, Gср∙10-3, кг/с |
||
|
G1 |
G2 |
G3 |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
14 |
1,95 |
0 |
325 |
321 |
314 |
320 |
|
2 |
14 |
1,95 |
– 1 |
181 |
176 |
183 |
180 |
|
3 |
14 |
1,95 |
– 2 |
101 |
106 |
108 |
105 |
|
4 |
14 |
1,95 |
– 3 |
40 |
35 |
36 |
37,5 |
Рассмотрим процесс сушки на примере поваренной соли. Требуется определить зависимость производительности (G) барабанного агрегата от скорости теплоносителя (ϑвх) на входе и угла наклона барабана (α). Экспериментальные данные приведены в таблице.
y1 = 92,25 + 299 R2 = 0,9664 или R = 0,9831 (12)
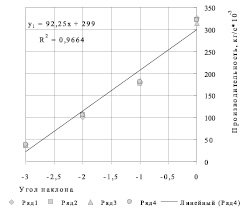
Рис. 1. Зависимость производительности сушилки от угла наклона барабана (вид уравнения линейный)
y2 = 9,5833х3 + 61,25х2 + 191,67 + 320 R2 = 1 или R = 1 (13)
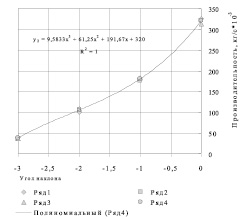
Рис. 2. Зависимость производительности сушилки от угла наклона барабана (вид уравнения полиномиального)
Из анализа уравнений (12), (13) и кривых на рис. 1, 2 видно, что связь между х и у уравнения полиномиального вида (13) сильнее, чем у уравнения линейного вида (12), следовательно, уравнение регрессии (13) адекватно эксперименту.



